20 Câu Trắc Nghiệm Trả Lời Ngắn Tính Đơn Điệu Của Hàm Số Giải Chi Tiết

20 câu trắc nghiệm trả lời ngắn tính đơn điệu của hàm số giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.

I. MỨC ĐỘ THÔNG HIỂU

1. HÀM BẬC BA

Câu 1:Cho hàm số $y = {x^3} – m{x^2} + 2x + 1$ với $m$ là tham số thực. Có bao nhiêu giá trị nguyên của $m$ để hàm số đồng biến trên tập số thực $mathbb{R}$?

Lời giải

Ta có $y’ = 3{x^2} – 2mx + 2.$

Hàm số đồng biến trên $mathbb{R}$$ Leftrightarrow y’ geqslant 0{text{ }}forall x in mathbb{R}$

$ Leftrightarrow Delta = {m^2} – 6m leqslant 0 Leftrightarrow m in left[ {0;6} right]$

Vì $m$ nguyên nên có 7 giá trị của $m$ thỏa mãn bài toán.

Câu 2:Cho hàm số $y = frac{1}{3}{x^3} + 2{x^2} + (m + 1)x + 2025$ Có bao nhiêu giá trị nguyên của $m in left[ {0;10} right]$ để hàm số đồng biến trên tập số thực $mathbb{R}$?

Lời giải

$y’ = {x^2} + 4x + left( {m + 1} right)$

Hàm số đồng biến trên $mathbb{R}$$ Leftrightarrow y’ geqslant 0,,forall x in mathbb{R}$

$ Leftrightarrow Delta ‘ leqslant 0 Leftrightarrow {2^2} – left( {m + 1} right) leqslant 0$$ Leftrightarrow m geqslant 3$

Do $m$ nguyên và $m in left[ {0;10} right]$ nên $m in left{ {3;4;5;6;7;8;9;10} right}$.

Vậy có $8$ giá trị của $m$ thỏa mãn bài toán.

Câu 3:Gọi $S$ là tập tất cả các số nguyên $m$ để hàm số $y = – frac{1}{3}{x^3} + m{x^2} + left( {5m – 6} right)x + {m^2}$ nghịch biến trên $mathbb{R}$. Tính tổng các phần tử của $S$.

Lời giải

Ta có: $y’ = – {x^2} + 2mx + 5m – 6$.

Hàm số đã cho nghịch biến trên $mathbb{R}$ khi và chỉ khi:

$y’ = – {x^2} + 2mx + 5m – 6 leqslant 0,forall x in mathbb{R} Leftrightarrow {m^2} + 5m – 6 leqslant 0 Leftrightarrow – 6 leqslant m leqslant 1$

Vì $m in mathbb{Z} Rightarrow m in left{ { – 6; – 5; – 4;…;1} right}$.

Vậy, tổng các phần tử của $S$ bằng $ – 6 + ( – 5) + ( – 4) + ( – 3) + ( – 2) + ( – 1) + 0 + 1 = – 20$

Câu 4:Cho hàm số $y = – {x^3} – m{x^2} + left( {4m + 9} right)x + 5$ với $m$ là tham số. Hỏi có bao nhiêu giá trị nguyên của $m$ để hàm số nghịch biến trên khoảng $left( { – infty ; + infty } right)$.

Lời giải

Ta có: $y’ = – 3{x^2} – 2mx + 4m + 9$

Hàm số nghịch biến trên $mathbb{R}$ khi $y’ leqslant 0,forall x in mathbb{R}$. Dấu “=” xảy ra tại hữu hạn điểm

$ Leftrightarrow – 3{x^2} – 2mx + 4m + 9 leqslant 0$

$ Leftrightarrow Delta ‘ = {m^2} + 12m + 27 leqslant 0 Leftrightarrow – 9 leqslant m leqslant – 3$

Mà $m in mathbb{Z} Rightarrow m in left{ { – 9; – 8;…; – 4; – 3} right}$

Vậy có $7$ giá trị của $m$ thỏa mãn bài toán.

Câu 5:Tìm số các giá trị nguyên của tham số $m$ để hàm số $y = frac{1}{3}m{x^3} – 2m{x^2} + left( {m – 5} right)x + 1$ nghịch biến trên $mathbb{R}$.

Lời giải

Ta có $y’ = m{x^2} – 4mx + m – 5$.

Hàm số nghịch biến trên $mathbb{R}$$ Leftrightarrow y’ leqslant 0,forall x in mathbb{R}$

TH1: $m = 0:y’ = – 5 < 0,forall x in mathbb{R}$ suy ra $m = 0$ thỏa mãn.

TH2: $m ne 0$: $left{ begin{gathered}
m < 0 hfill \
Delta ‘ leqslant 0 hfill \
end{gathered} right. Leftrightarrow left{ begin{gathered}
m < 0 hfill \
3{m^2} + 5m leqslant 0 hfill \
end{gathered} right. Leftrightarrow – frac{5}{3} leqslant m < 0$.

Vậy $ – frac{5}{3} leqslant m leqslant 0xrightarrow{{m in mathbb{Z}}}m in left{ { – 1;0} right}$.

Vậy có $2$ giá trị của $m$ thỏa mãn bài toán.

Câu 6: Cho hàm số $fleft( x right)$ có đạo hàm là $f’left( x right) = left( {x – 1} right)left( {x – m} right)$ với $m$ là tham số thực. Hỏi có bao nhiêu giá trị nguyên của $m$ để hàm số $y = f(x)$ nghịch biến trên khoảng $left( { – infty ; + infty } right)$.

Lời giải

Hàm số đồng biến trên $left( { – infty ; + infty } right)$ khi

$f’left( x right) geqslant 0,forall x in mathbb{R} Leftrightarrow left( {x – 1} right)left( {x – m} right) geqslant 0,forall x in mathbb{R}$

$ Leftrightarrow {x^2} – left( {m + 1} right)x + m geqslant 0,forall x in mathbb{R}$

$ Leftrightarrow left{ begin{gathered}
a = 1 > 0 hfill \
Delta = {left( {m + 1} right)^2} – 4m leqslant 0 hfill \
end{gathered} right.$

$ Leftrightarrow {m^2} – 2m + 1 leqslant 0$

$ Leftrightarrow {left( {m – 1} right)^2} leqslant 0 Leftrightarrow m – 1 = 0 Leftrightarrow m = 1$.

Vậy có $1$ giá trị của $m$ thỏa mãn bài toán.

2. HÀM PHÂN THỨC

Câu 1:Cho hàm số $y = frac{{mx – 5m}}{{x – m}}$ với $m$ là tham số. Gọi $S$ là tập hợp tất cả các giá trị nguyên của $m$ để hàm số đồng biến trên mỗi khoảng xác định. Tìm số phần tử của $S$.

Lời giải

Ta có: $y’ = frac{{ – {m^2} + 5m}}{{{{left( {x – m} right)}^2}}}$

Hàm số đồng biến trên mỗi khoảng xác định$ Leftrightarrow – {m^2} + 5m > 0 Leftrightarrow 0 < m < 5$.

Do m nguyên nên $m in left{ {1;2;3;4} right}$.

Vậy, có $4$ giá trị của $m$ thỏa mãn bài toán.

Câu 2:Cho hàm số $y = frac{{x + 3m}}{{2x + {m^2}}}$ với $m$ là tham số. Gọi $S$ là tập hợp tất cả các giá trị nguyên của $m$ để hàm số nghịch biến trên từng khoảng xác định. Tìm số phần tử của $S$.

Lời giải

Ta có: $y’ = frac{{{m^2} – 6m}}{{{{left( {2x – {m^2}} right)}^2}}}$

Hàm số nghịch biến trên mỗi khoảng xác định$ Leftrightarrow {m^2} – 6m < 0 Leftrightarrow 0 < m < 6$.

Do m nguyên nên $m in left{ {1;2;3;4;5} right}$.

Vậy, có $5$ giá trị của $m$ thỏa mãn bài toán.

Câu 3:Cho hàm số $y = frac{{3{x^2} – m}}{{x – 1}}$ với $m$ là tham số. Gọi $S$ là tập hợp tất cả các giá trị nguyên của $m$ thuộc khoảng $left( {0;10} right)$ hàm số đồng biến trên mỗi khoảng xác định. Tìm số phần tử của $S$.

Lời giải

Ta có: $y’ = frac{{3{x^2} – 6x + m}}{{{{left( {x – m} right)}^2}}}$

Hàm số đồng biến trên mỗi khoảng xác định

$ Leftrightarrow 3{x^2} – 6x + m geqslant 0,,forall x in mathbb{R} Leftrightarrow Delta ‘ leqslant 0$

$ Leftrightarrow 9 – 3m leqslant 0 Leftrightarrow m geqslant 3$

Do m nguyên và $m in left( {0;10} right)$nên $m in left{ {3;4;5;6;7;8;9} right}$.

Vậy, có $7$ giá trị của $m$ thỏa mãn bài toán.

II. MỨC ĐỘ VẬN DỤNG

1. HÀM BẬC BA

Câu 1:Cho hàm số $y = frac{1}{3}{x^3} – frac{1}{2}(m + 1){x^2} + mx$ với $m$ là tham số thực. Có bao nhiêu giá trị nguyên của tham số $m in left[ {2;15} right]$ để hàm số đã cho đồng biến trên khoảng $left( {12; + infty } right)?$

Lời giải

Tập xác định của hàm số đã cho là $D = mathbb{R}$

Ta có: $y’ = {x^2} – (m + 1)x + m$

$y’ = 0 Leftrightarrow {x^2} – (m + 1)x + m = 0 Leftrightarrow left[ begin{gathered}
x = 1 hfill \
x = m hfill \
end{gathered} right.$

Do $m in left[ {2;15} right]$ nên $m > 1$. Ta có bảng biến thiên

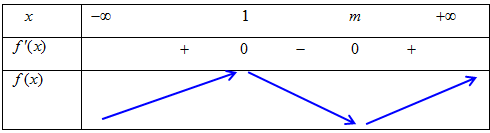
Hàm số đồng biến trên $left( {5; + infty } right) Leftrightarrow m leqslant 12$.

Do m nguyên và $m in left[ {2;15} right]$ nên $m in left{ {2;3;4;5;6;7;8;9;10;11;12} right}$.

Vậy, có $11$ giá trị của $m$ thỏa mãn bài toán.

Câu 2:Cho hàm số $y = – frac{1}{3}{x^3} + frac{1}{2}(2 – m){x^2} + 2mx + 2025$ với $m$ là tham số thực. Có bao nhiêu giá trị nguyên của tham số $m in left( {2;15} right)$ để hàm số đã cho đồng biến trên khoảng $left( { – 6;2} right)?$

Lời giải

Tập xác định của hàm số đã cho là $D = mathbb{R}$

Ta có: $y’ = – {x^2} + (2 – m)x + 2m$

$y’ = 0 Leftrightarrow – {x^2} + (2 – m)x + 2m = 0 Leftrightarrow left[ begin{gathered}
x = 2 hfill \
x = – m hfill \
end{gathered} right.$

Do $m in left( {2;15} right)$ nên $ – m < 2$. Ta có bảng biến thiên

Hàm số đồng biến trên $left( { – 6;2} right) Leftrightarrow – m leqslant – 6 Leftrightarrow m geqslant 6$.

Do m nguyên và $m in left( {2;15} right)$ nên $m in left{ {6;7;8;9;10;11;12;13;14} right}$.

Vậy, có $9$ giá trị của $m$ thỏa mãn bài toán.

2. HÀM PHÂN THỨC

Câu 1:Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = frac{{x + 4}}{{x + m}}$ đồng biến trên khoảng $left( { – infty ,;, – 7} right)$?

Lời giải

Chọn B

Tập xác định: $D = mathbb{R}backslash left{ { – m} right}$.

Ta có: $y’ = frac{{m – 4}}{{{{left( {x + m} right)}^2}}}$.

Hàm số đã cho đồng biến trên khoảng $left( { – infty ,;, – 7} right)$ $ Leftrightarrow y’ > 0$, $forall x in left( { – infty ,;, – 7} right)$ $ Leftrightarrow left{ begin{gathered}
m – 4 > 0 hfill \
– m notin left( { – infty ,;, – 7} right) hfill \
end{gathered} right.$$ Leftrightarrow left{ begin{gathered}
m > 4 hfill \
– m geqslant – 7 hfill \
end{gathered} right. Leftrightarrow left{ begin{gathered}
m > 4 hfill \
m leqslant 7 hfill \
end{gathered} right. Leftrightarrow 4 < m leqslant 7$.

Do m nguyên nên $m in left{ {5;6;7} right}$.

Vậy, có $3$ giá trị của $m$ thỏa mãn bài toán.

Câu 2: Cho hàm số $y = frac{{x + 1}}{{x – m}},$ với $m$ là tham số thực. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số đã cho nghịch biến trên khoảng $left( {2; + infty } right)?$

Lời giải

Tập xác định của hàm số đã cho là $D = mathbb{R}backslash left{ m right}.$

Ta có $y’ = frac{{ – m – 1}}{{{{left( {x – m} right)}^2}}},forall x in D.$

Hàm số nghịch biến trên $left( {2; + infty } right) Leftrightarrow left{ begin{gathered}
y’ < 0{text{ }}forall x in left( {2; + infty } right) hfill \
left( {2; + infty } right) subset D hfill \
end{gathered} right. Leftrightarrow left{ begin{gathered}
– m – 1 < 0 hfill \
m leqslant 2 hfill \
end{gathered} right. Leftrightarrow – 1 < m leqslant 2$

Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu.

Câu 3:Cho hàm số $y = frac{{mx – 2m – 3}}{{x – m}}$ với $m$ là tham số. Gọi $S$ là tập hợp tất cả các giá trị nguyên của $m$ để hàm số đồng biến trên khoảng $left( {2; + infty } right)$. Tìm số phần tử của $S$.

Lời giải

Ta có $y’ = frac{{ – {m^2} + 2m + 3}}{{{{left( {x – m} right)}^2}}}$.

Để thoả mãn ta có $left{ begin{gathered}
– {m^2} + 2m + 3 > 0 hfill \
m leqslant 2 hfill \
end{gathered} right. Leftrightarrow left{ begin{gathered}
– 1 < m < 3 hfill \
m leqslant 2 hfill \
end{gathered} right. Leftrightarrow – 1 < m leqslant 2$.

$ Rightarrow S = left{ {0;1;2} right}$.

Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu.

Câu 4:Cho hàm số $y = frac{{2x + 12}}{{x + m}}$ (m là tham số). Có tất cả bao nhiêu giá trị nguyên của m để hàm số đã cho nghịch biến trên khoảng $left( {2; + infty } right)$?

Lời giải

Ta có $y = frac{{2x + 12}}{{x + m}} Rightarrow y’ = frac{{2m – 12}}{{{{left( {x + m} right)}^2}}}$ với $x ne – m$.

Để hàm số nghịch biến trên $left( {2; + infty } right)$$ Leftrightarrow y’ < {0^{}}forall x in left( {2; + infty } right) Leftrightarrow left{ {begin{array}{*{20}{c}}
{2m – 12 < 0} \
{x ne – m}
end{array},x in left( {2; + infty } right)} right.$

$ Leftrightarrow y’ < {0^{}}forall x in left( {2; + infty } right) Leftrightarrow left{ {begin{array}{*{20}{c}}
{2m – 12 < 0} \
{ – m leqslant 2}
end{array}} right. Leftrightarrow left{ {begin{array}{*{20}{c}}
{m < 6} \
{m geqslant – 2}
end{array}} right. Leftrightarrow – 2 leqslant m < 6$.

Vậy có $8$ giá trị nguyên của m thỏa mãn yêu cầu.

Câu 5:Cho hàm số $y = frac{{cos x – 3}}{{cos x – m}}$. Có tất cả bao nhiêu giá trị nguyên dương của m nghịch biến trên khoảng $left( {frac{pi }{2};pi } right)$?

Lời giải

Xét $m = 3$ khi đó, $y = 1$ nên không thỏa mãn

Xét $m ne 3$:

Ta có: $y’ = – sin x.frac{{ – m + 3}}{{{{left( {cos x – m} right)}^2}}} leqslant 0 Rightarrow sin x.left( {m – 3} right) leqslant 0$

Vì $x in left( {frac{pi }{2};pi } right)$ nên $sin x > 0 Rightarrow m – 3 leqslant 0 Rightarrow m leqslant 3$

Mà $m ne 3 Rightarrow m < 3$

Với $x in left( {frac{pi }{2};pi } right) Rightarrow cos x in left( { – 1;0} right).$ Do đó điều kiện $cos x ne m Leftrightarrow left[ begin{gathered}
m geqslant 0 hfill \
m leqslant – 1 hfill \
end{gathered} right.$

Suy ra, $left[ begin{gathered}
0 leqslant m < 3 hfill \
m leqslant – 1 hfill \
end{gathered} right.$

Vậy có $2$ giá trị nguyên dương của m thỏa mãn yêu cầu.

Câu 6:Có bao nhiêu số nguyên dương của tham số $m$ để hàm số $y = frac{{cos x + 1}}{{10cos x + m}}$ đồng biến trên khoảng $left( {0,;,frac{pi }{2}} right)$ ?

Lời giải

Đặt $cos x = t$

Bài toán trở thành: Tìm $m$ để hàm số nghịch biến trên $left( {0;1} right)$

* $y = frac{{t + 1}}{{10t + m}}left( {t ne – frac{m}{{10}}} right)$

* $y’ = frac{{m – 10}}{{{{left( {10t + m} right)}^2}}}$

* Hàm số nghịch biến trên $left( {0;1} right) Leftrightarrow y’ < 0left( {forall t in left( {0;1} right)} right)$

$ Leftrightarrow left{ begin{gathered}
m – 10 < 0 hfill \
– frac{m}{{10}} notin left( {0;1} right) hfill \
end{gathered} right. Leftrightarrow left{ begin{gathered}
m < 10 hfill \
left[ begin{gathered}
– frac{m}{{10}} leqslant 0 hfill \
– frac{m}{{10}} geqslant 1 hfill \
end{gathered} right. hfill \
end{gathered} right. Leftrightarrow left{ begin{gathered}
m < 10 hfill \
left[ begin{gathered}
m geqslant 10 hfill \
m leqslant – 10 hfill \
end{gathered} right. hfill \
end{gathered} right.$

$ Rightarrow left[ begin{gathered}
0 leqslant m < 10 hfill \
m leqslant – 10 hfill \
end{gathered} right. Rightarrow left{ begin{gathered}
m in N* hfill \
m in left{ {1,2,3,4,5,6,7,8,9} right} hfill \
end{gathered} right. Rightarrow $ 9 giá trị.

Vậy có $9$ giá trị của m thỏa mãn yêu cầu.

3. HÀM SỐ KHÁC

Câu 1:Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số $y = left| {3{x^4} – m{x^3} + 6{x^2} + m – 3} right|$ đồng biến trên khoảng $left( {0; + infty } right)$?

Lời giải

$fleft( x right) = 3{x^4} – m{x^3} + 6{x^2} + m – 3$

Do $mathop {lim }limits_{x to + infty } fleft( x right) = + infty > 0$ nên $left| {fleft( x right)} right|$ đồng biến trên $left( {0; + infty } right)$

$left{ begin{gathered}
fleft( x right) > 0 hfill \
f’left( x right) > 0 hfill \
end{gathered} right.,forall x in left( {0; + infty } right) Leftrightarrow left{ begin{gathered}
fleft( x right) geqslant 0 hfill \
f’left( x right) geqslant 0 hfill \
end{gathered} right.,forall x in left( {0; + infty } right)$

$ Leftrightarrow left{ begin{gathered}
m – 3 geqslant 0 hfill \
12{x^3} – 3m{x^2} + 12x geqslant 0 hfill \
end{gathered} right.,forall x in left( {0; + infty } right) Leftrightarrow left{ begin{gathered}
m geqslant 3 hfill \
m leqslant 4x + frac{4}{x} hfill \
end{gathered} right.,forall x in left( {0; + infty } right)$

$ Leftrightarrow left{ begin{gathered}
m geqslant 3 hfill \
m leqslant mathop {min }limits_{left( {0; + infty } right)} left( {4x + frac{4}{x}} right) hfill \
end{gathered} right. Leftrightarrow left{ begin{gathered}
m geqslant 3 hfill \
m leqslant 8 hfill \
end{gathered} right. Leftrightarrow 3 leqslant m leqslant 8$

Do $m in Z Rightarrow m in left{ {3,4,5,6,7,8} right}.$

Vậy có $6$ giá trị nguyên dương của m thỏa mãn yêu cầu.

Câu 2:Cho hàm số $fleft( x right)$ có đạo hàm trên $mathbb{R}$ là $f’left( x right) = left( {x – 1} right)left( {x + 3} right).$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $left[ { – 10;20} right]$ để hàm số $y = fleft( {{x^2} + 3x – m} right)$ đồng biến trên khoảng $left( {0;2} right)$?

Hàm số $y = fleft( x right)$ nghịch biến trên $left( {a;b} right)$ khi $f’left( x right) leqslant 0,forall x in left( {a;b} right).$ Dấu “=” xảy ra tại hữu hạn điểm

Lời giải

Ta có: $y’ = f’left( {{x^2} + 3x – m} right)left( {2x + 3} right)$

Với $x in left( {0;2} right) Rightarrow 2x + 3 > 0$

Lại có: $f’left( x right) = left( {x – 1} right)left( {x + 3} right)$. Khi đó $f’left( x right) geqslant 0 Leftrightarrow left[ begin{gathered}
x leqslant – 3 hfill \
x geqslant 1 hfill \
end{gathered} right.;f’left( x right) < 0 Leftrightarrow – 3 < x < 1$

Hàm số đồng biến trên khoảng $left( {0;2} right)$ khi

$y’ geqslant 0 Leftrightarrow left( {2x + 3} right)f’left( {{x^2} + 3x – m} right) geqslant 0 Leftrightarrow f’left( {{x^2} + 3x – m} right) geqslant 0$

$ Leftrightarrow left[ begin{gathered}
{x^2} + 3x – m leqslant – 3 hfill \
{x^2} + 3x – m geqslant 1 hfill \
end{gathered} right. Leftrightarrow left[ begin{gathered}
m geqslant {x^2} + 3x + 3 hfill \
m leqslant {x^2} + 3x – 1 hfill \
end{gathered} right.$

$ Leftrightarrow left[ begin{gathered}
m geqslant mathop {max }limits_{left( {0;2} right)} left( {{x^2} + 3x + 3} right) hfill \
m leqslant mathop {min }limits_{left( {0;2} right)} {x^2} + 3x – 1 hfill \
end{gathered} right. Leftrightarrow left[ begin{gathered}
m geqslant 13 hfill \
m leqslant – 1 hfill \
end{gathered} right.$

Mà $m in mathbb{Z},m in left[ { – 10;20} right]$ nên $m in left{ { – 10; – 9;…; – 1;13;14;…;19;20} right}$.

Câu 3:Cho hàm số $y = fleft( x right)$. Đồ thị hàm số $y = f’left( x right)$ như hình bên dưới. Hỏi hàm số $gleft( x right) = fleft( {{x^2} – 5} right)$ có bao nhiêu khoảng nghịch biến ?

Lời giải

$g’left( x right) = 2x.f’left( {{x^2} – 5} right) = 0 Rightarrow left[ begin{gathered}
x = 0 hfill \
{x^2} – 5 = – 4 hfill \
{x^2} – 5 = – 1 hfill \
{x^2} – 5 = 2 hfill \
end{gathered} right. Rightarrow left[ begin{gathered}
x = 0 hfill \
x = pm 1 hfill \
x = pm 2 hfill \
x = pm sqrt 7 hfill \
end{gathered} right.$

$ Rightarrow $ Hàm số có 4 khoảng nghịch biến.