Giải Toán 12 Cánh Diều Bài 4 Chương 4 Ứng Dụng Hình Học Của Tích Phân

Câu 1.Hình thang cong $ABCD$ ở Hình 28 có diện tích bằng:
A. $int_1^2 {left( {frac{4}{x} – x + 3} right)} dx$

B. $int_1^2 {left( {frac{4}{x} + x + 3} right)} dx$.

C. $int_1^2 {left( {frac{4}{x} – x – 3} right)} dx$.

D. $int_2^4 {left( {frac{4}{x} + x + 3} right)} dx$.

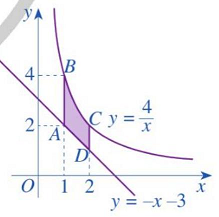
Hình 28

Lời giải

Câu 2.Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số $fleft( x right) = sqrt x $, trục hoành và hai đường thẳng $x = 0,x = 2$ quay quanh trục $Ox$ là:
A. $pi int_0^2 {sqrt x } ;dx$.

B. $pi int_0^2 x ;dx$.

C. $int_0^2 {sqrt x } ;dx$.

D. $int_0^2 x ;dx$.

Lời giải

Câu 3.Cho đồ thị hàm số $y = {e^x}$ và hình phẳng được tô màu như Hình 29.

a) Hình phẳng đó được giới hạn bởi các đường nào?

b) Tính diện tích hình phẳng đó.

Hình 29

Lời giải

Câu 4.Cho đồ thị các hàm số $y = {left( {frac{1}{2}} right)^x},y = x + 1$ và hình phẳng được tô màu như Hình 30.

a) Hình phẳng đó được giới hạn bởi các đường nào?

b) Tính diện tích hình phẳng đó.

Hình 30

Lời giải

Câu 5.Cho đồ thị hàm số $y = frac{1}{x}$ và khối tròn xoay như Hình 31.

a) Hình phẳng được giới hạn bởi các đường nào để khi quay quanh trục $Ox$ ta được khối tròn xoay như Hình 31 ?

b) Tính thể tích khối tròn xoay đó.

Hình 31

Lời giải

Câu 6. Cho đồ thị hàm số $y = fleft( t right)$ như Hình 32.

a) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = fleft( t right)$, trục $Ot$ và hai đường thẳng $t = 0$, $t = 2$.

b) Hỏi $intlimits_0^1 {f(u)du} $biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường nào trong Hình 32?

Hình 32

Lời giải

Câu 7. Người ta dự định lắp kính cho củ̉a của một mái vòm có dạng hình parabol. Hãy tính diện tích mặt kính cần lắp vào, biết rằng vòm cửa cao $21;m$ và rộng 70 m (Hình 33).

(Nguồn: https://shutterstock.com)

Hình 33

Lời giải

Câu 8. Hình 34 minh hoạ mặt cắt đứng của một con kênh đặt trong hệ trục toạ độ $Oxy$. Đáy của con kênh là một đường cong cho bởi phương trình

$y = fleft( x right) = frac{3}{{100}}left( { – frac{1}{3}{x^3} + 5{x^2}} right).;$

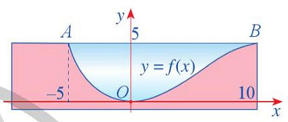
Hình 34

Hãy tính diện tích hình phẳng tô màu xanh trong Hình 34 , biết đơn vị trên mỗi trục toạ độ là mét.

Lời giải

Câu 9. Cho tam giác vuông $OPM$ có cạnh $OP$ nằm trên trục $Ox$.

Giả sử $widehat {POM} = alpha ,OM = lleft( {0 leqslant alpha leqslant frac{pi }{3};l > 0} right)$.

Gọi $mathcal{N}$ là khối tròn xoay thu được khi quay tam giác đó xung quanh trục $Ox$ (Hình 35). Tính thể tích của $mathcal{N}$ theo $alpha $ và $l$.

Lời giải

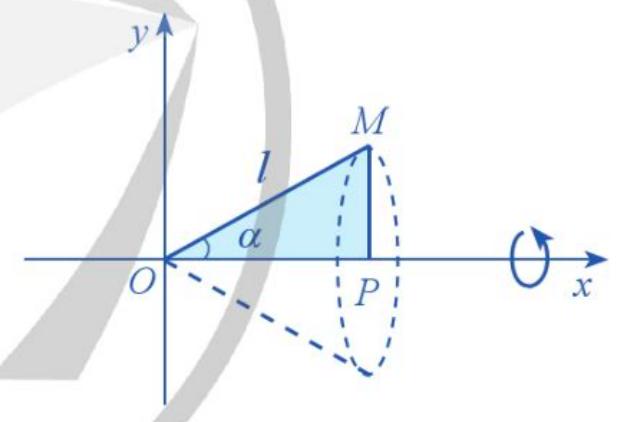
Hình 35

Câu 10.Sau khi đo kích thước của thùng rượu vang (Hình 36), bạn Quân xác định thùng rượu vang có dạng hình tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số $y = – 0,011{x^2} – 0,071x + 40$trục $Ox$ và hai đường thẳng $x = – 35,x = 35$ quay quanh trục $Ox$. Tính thể tích thùng rượu vang đó, biết đơn vị trên mỗi trục toạ độ là centimét.

(Nguồn: https://shutterstock.com)

Hình 36

Lời giải

Giải Toán 12 Cánh Diều Bài 4 Chương 4 Ứng Dụng Hình Học Của Tích Phân