20 Câu Hỏi Trả Lời Ngắn GTLN Và GTNN Của Hàm Số Lớp 12 Giải Chi Tiết

20 câu hỏi trả lời ngắn GTLN và GTNN của hàm số lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

Câu 1: Tìm giá trị nhỏ nhất của hàm số $fleft( x right) = frac{{x + 3}}{{x + 1}}$ trên khoảng $left( {1;4} right]$.

Lời giải

Tập xác định: $D = mathbb{R}backslash left{ { – 1} right}$.

$f’left( x right) = frac{{ – 2}}{{{{left( {x + 1} right)}^2}}} < 0,,forall x in left( {1;4} right]$.

Bảng biến thiên:

Từ bảng biến thiên ta có $mathop {min }limits_{left( {1;4} right]} f(x) = f(4) = frac{7}{5}$.

Trả lời: $frac{7}{5}$

Câu 2: Tìm giá trị lớn nhất của hàm số $fleft( x right) = {x^3} – 2{x^2} + x – 6$ trên khoảng $left( { – 1:1} right)$.

Lời giải

Tập xác định: $D = mathbb{R}$, ta chỉ xét trên khoảng $left( { – 1;1} right)$.

$y’ = 3{x^2} – 4x + 1$; $y’ = 0 Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 1} \
{x = frac{1}{3}}
end{array}} right.$

Bảng biến thiên:

Từ bảng biến thiên ta có .

Trả lời: $ – frac{{158}}{{27}}$

Câu 3:Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $fleft( x right) = frac{x}{{4 + {x^2}}}$ trên $mathbb{R}$.

Lời giải

Trả lời: $frac{1}{4}$

Tập xác định: $mathcal{D} = mathbb{R}$, ta chỉ xét trên nửa khoảng $left[ {frac{1}{2}; + infty } right)$.

Đạo hàm: $f’left( x right) = {x^2}left( {1 – x} right)left( {3 – 5x} right)$;

$f’left( x right) = 0 Leftrightarrow x = 0,x = 1,x = frac{3}{5}$.

Bảng biến thiên:

Từ bảng biến thiên ta có $mathop {min }limits_mathbb{R} fleft( x right) = fleft( { – 2} right) = – frac{1}{4}$ và .

Câu 4: Tìm giá trị nhỏ nhất $m$ của hàm số $fleft( x right) = sqrt {x + frac{1}{x}} $ trên khoảng $left( {0; + infty } right)$.

Lời giải

Trả lời: $sqrt 2 $

Đạo hàm $f’left( x right) = frac{{1 – frac{1}{{{x^2}}}}}{{2sqrt {x + frac{1}{x}} }} = frac{{{x^2} – 1}}{{2{x^2}sqrt {x + frac{1}{x}} }}$

$f’left( x right) = 0 Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = – 1 notin left( {0; + infty } right)} \
{x = 1 in left( {0; + infty } right)}
end{array}} right.$.

Bảng biến thiên

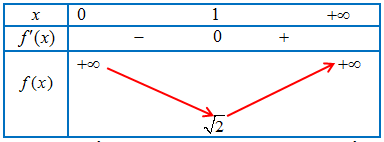
Từ bảng biến thiên ta tìm được giá trị nhỏ nhất của hàm số là $fleft( 1 right) = sqrt 2 $.

Câu 5: Tìm giá trị nhỏ nhất $m$ của hàm số $fleft( x right) = {x^2} + frac{2}{x}$ trên khoảng $left( {0; + infty } right)$.

Lời giải

Trả lời: 3

Đạo hàm $f’left( x right) = 2x – frac{2}{{{x^2}}} = frac{{2left( {{x^3} – 1} right)}}{{{x^2}}}$$ Rightarrow f’left( x right) = 0 Leftrightarrow x = 1 in left( {0; + infty } right)$.

Lập bảng biến thiên và dựa vào bảng biến thiên ta thấy .

Câu 6:Cho hàm số $y = frac{{mx – 1}}{{x + m}}$. Tìm $m$ để hàm số đạt giá trị lớn nhất trên đoạn $left[ {1;4} right]$ bằng 1 .

Lời giải

Trả lời: $frac{5}{3}$

Tập xác dịnh của hàm số: $mathcal{D} = mathbb{R} setminus left{ { – m} right}$.

Ta có: $y’ = frac{{{m^2} + 1}}{{{{(x + m)}^2}}} > 0,forall x in mathcal{D}$ nên hàm số luôn đồng biến trên trên khoảng xác định của nó.

Do đó $mathop {max}limits_{left[ {1;4} right]} y = f(4) = frac{{4m – 1}}{{4 + m}} = 1$$ Leftrightarrow 4m – 1 = 4 + m Leftrightarrow m = frac{5}{3}$.

Thử lại ta thấy $m = frac{5}{3}$ là giá trị thỏa mãn yêu cầu bài toán.

Câu 7: Cho hàm số $fleft( x right) = msqrt {x – 1} $. Gọi ${m_1},{m_2}$ là hai giá trị của $m$ thỏa mãn $mathop {min }limits_{left[ {2;5} right]} f(x) + mathop {max}limits_{left[ {2;5} right]} f(x) = {m^2} – 10$. Tính ${m_1} + {m_2}$

Lời giải

Trả lời: 3

Với mọi $x in left[ {2;5} right]$ có $f’left( x right) = frac{m}{{2sqrt {x – 1} }}$. Ta thấy dấu của $f’left( x right)$ phụ thuộc vào dấu của $m$

$forall m ne 0$ thì $fleft( x right)$ đơn điệu trên $left[ {2;5} right]$

Từ giả thiết ta được ${m^2} – 10 = m + 2m Leftrightarrow {m^2} – 3m – 10 = 0$

$ Leftrightarrow left[ {begin{array}{*{20}{l}}
{m = 5} \
{m = – 2}
end{array}} right.$.

Vậy ${m_1} + {m_2} = 3$.

Câu 8:Cho hàm số $fleft( x right) = {x^3} + left( {{m^2} + 1} right)x + {m^2} – 2$ với $m$ là tham số thực. Tìm tất cả các giá trị thực dương $m$ để hàm số có giá trị nhỏ nhất trên đoạn $left[ {0;2} right]$ bằng 7 .

Lời giải

Trả lời: 3

Đạo hàm $f’left( x right) = 3{x^2} + {m^2} + 1 > 0,forall x in mathbb{R}$.

Suy ra hàm số $fleft( x right)$ đồng biến trên $left[ {0;2} right]$

$ Rightarrow mathop {min }limits_{left[ {0;2} right]} fleft( x right) = fleft( 0 right) = {m^2} – 2$.

Theo bài ra: $mathop {min }limits_{left[ {0;2} right]} fleft( x right) = 7 Leftrightarrow {m^2} – 2 = 7$$ Leftrightarrow m = pm 3$.

Ta chọn $m = 3$

Câu 9: Cho hàm số $y = fleft( x right) = a{x^4} + b{x^2} + c$ xác định và liên tục trên $mathbb{R}$ và có bảng biến thiên sau

Tìm giá trị nhỏ nhất của hàm số $y = fleft( {x + 3} right)$ trên đoạn $left[ {0;2} right]$.

Lời giải

Trả lời: 66

Hàm số có dạng $fleft( x right) = a{x^4} + b{x^2} + c$. Từ bảng biến thiên ta có

$left{ {begin{array}{*{20}{l}}
{fleft( 0 right) = 3} \
{fleft( 1 right) = 2} \
{f’left( 1 right) = 0}
end{array} Leftrightarrow left{ {begin{array}{*{20}{l}}
{c = 3} \
{a + b + c = 2} \
{4a + 2b = 0}
end{array}} right.} right.$

$ Leftrightarrow left{ {begin{array}{*{20}{l}}
{c = 3} \
{b = – 2} \
{a = 1}
end{array}} right.$$ Rightarrow fleft( x right) = {x^4} – 2{x^2} + 3$.

Đặt $t = x + 3,x in left[ {0;2left] { Leftrightarrow t in } right[3;5} right]$.

Dựa vào đồ thị, hàm số $y = fleft( t right)$ đồng biến trên đoạn $left[ {3;5} right]$.

Do đó .

Câu 10: Cho hàm $fleft( x right)$ liên tục trên đoạn $left[ { – 4;4} right]$ và có bảng biến thiên như hình vẽ bên dưới.

Có tất cả bao nhiêu giá trị thực của tham số $m$ thuộc đoạn $left[ { – 4;4} right]$ để hàm số $gleft( x right) = left| {fleft( {{x^3} + 2x} right) + 3fleft( m right)} right|$ có giá trị lớn nhất trên đoạn $left[ { – 1;1} right]$ bằng 8 ?

Lời giải

Trả lời: 11

Đặt $t = fleft( {{x^3} + 2x} right)$. Vì $x in left[ { – 1;1} right]$ nên $t in left[ { – 6;5} right]$.

Khi đó, $gleft( x right) = left| {t + 3fleft( m right)} right|$ với $t in left[ { – 6;5} right]$

Xét hàm số $h(t) = t + 3fleft( m right)$

Ta có: $h'(t) = 1 > 0,,forall t in left[ { – 6;5} right]$.

Suy ra, $mathop {max}limits_{left[ { – 6;5} right]} = h(5) = 5 + 3f(m)$ và $mathop {min }limits_{left[ { – 6;5} right]} = h( – 6) = – 6 + 3f(m)$

Do đó, $mathop {max}limits_{left[ { – 1;1} right]} g(x) = mathop {max}limits_{left[ { – 6;15} right]} left| {h(t)} right|$

$ = frac{{left| {left( {5 + 3f(m)} right) + left( { – 6 + 3f(m)} right)} right| + left| {left( {5 + 3f(m)} right) – left( { – 6 + 3f(m)} right)} right|}}{2}$

$ = frac{{left| {6f(m) – 1} right| + 11}}{2}$.

Theo đề,

$ Leftrightarrow left[ begin{gathered}
6f(m) – 1 = 5 hfill \
6f(m) – 1 = – 5 hfill \
end{gathered} right. Leftrightarrow left[ begin{gathered}
f(m) = 1 hfill \
f(m) = – frac{2}{3} hfill \
end{gathered} right.$

Với $fleft( m right) = 1$, dựa vào bảng biến thiên suy ra có 5 giá trị của $m$.

Với $fleft( m right) = frac{{ – 2}}{3}$, dựa vào bảng biến thiên suy ra có 6 giá trị của $m$.

Vậy có 11 giá trị của $m$ thỏa mãn yêu cầu đề bài.

Chú ý: Để tìm Giá trị lớn nhất và nhỏ nhất của hàm số $y = | f(x)|$ ta làm như sau:

Bước 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$.

Giả sử $mathop {min }limits_D f(x) = m$; $mathop {max }limits_D f(x) = M$.

Bước 2: Khi đó,

$mathop {max}limits_D |f(x)| = frac{{|M + m| + |M – m|}}{2}$;

$mathop {min }limits_D |f(x)| = left{ {begin{array}{*{20}{l}}
{frac{{|M + m| – |M – m|}}{2}}&{ khi,,m.M > 0} \
0&{ khi,,m.M leqslant 0}
end{array}} right.$.

Câu 11: Độ giảm huyết áp của một bệnh nhân được cho bởi công thức $Fleft( x right) = frac{1}{{40}}{x^2}left( {30 – x} right)$, trong đó $x$ là liều lượng thuốc tiêm cho bệnh nhân . Liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là ?.

Lời giải

Trả lời: 20

Xét hàm số : $Fleft( x right) = frac{1}{{40}}{x^2}left( {30 – x} right);(x > 0)$.

$ Rightarrow F’left( x right) = frac{1}{{40}} cdot 2xleft( {30 – x} right) – frac{1}{{40}}{x^2} = frac{1}{{40}}left( { – 3{x^2} + 60x} right)$.

$F'(x) = 0 Leftrightarrow frac{1}{{40}}left( { – 3{x^2} + 60x} right) = 0$$ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0,,,(loai)} \
{x = 20}
end{array}} right.$

Bảng biến thiên

Dựa vào BBT ta thấy để huyết áp giảm nhiều nhất thì liều lượng thuốc cần tiêm cho bệnh nhân là $x = 20$.

Câu 12: Sau khi phát hiện ra dịch bệnh vi rút Zika, các chuyên gia sở y tế TP.HCM ước tính số người nhiễm bệnh kể từ khi xuất hiện bệnh nhân đầu tiên đến ngày thứ $t$ là $fleft( t right) = 15{t^2} – {t^3}$. Ta xem $f’left( t right)$ là tốc độ truyền bệnh tại thời điểm $t$. Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ bao nhiêu?

Lời giải

Trả lời: 5

Ta có: $fleft( t right) = 15{t^2} – {t^3}$.

$f’left( t right) = 30t – 3{t^2} = – 3{(t – 5)^2} + 75 leqslant 75$.

Suy ra $f'{(t)_{max}} = 75 Leftrightarrow t = 5$.

Câu 13: Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng $8;{m^3}$, thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là $100000/{m^2}$, giá tôn làm thành xung quanh thùng là $50000/{m^2}$. Hỏi người bán gạo đó cần đóng thùng đựng gạo với cạnh đáy là bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất?.

Lời giải

Trả lời: 2

Gọi cạnh đáy và cạnh bên của thùng tôn là $a$ và $b$.

Ta có thể tích thùng tôn là: $V = {a^2}b = 8$. Suy ra: $b = frac{8}{{{a^2}}}$.

Chi phí để sản xuất thùng tôn là: $4ab.50000 + 100000{a^2}$

$ = frac{{1600000}}{a} + 100000{a^2}$.

Khảo sát hàm $y = frac{{1600000}}{a} + 100000{a^2}$ với $a > 0$.

Suy ra: $y’ = – frac{{1600000}}{{{a^2}}} + 200000a = 0 Leftrightarrow a = 2$.

Khi đó, ta có bảng biến thiên sau:

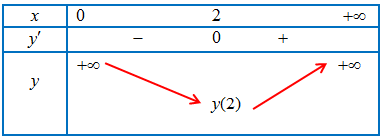
Dựa vào bảng biến thiên ta có ${y_{min;}} Leftrightarrow a = 2$

Câu 14: Người ta muốn mạ vàng cho một cái hộp có đáy hình vuông không nắp có thể tích là 4 lít. Tìm kích thước của hộp đó để lượng vàng dùng mạ là ít nhất. Giả sử độ dày của lớp mạ tại mọi nơi trên mặt ngoài hộp là như nhau.

Lời giải

Trả lời: 2

Gọi $x$ là cạnh của đáy hộp.

$h$ là chiều cao của hộp.

$Sleft( x right)$ là diện tích phần hộp cần mạ.

Khi đó, khối lượng vàng dùng mạ tỉ lệ thuận với $S$.

Ta có: $Sleft( x right) = {x^2} + 4xh,,left( 1 right)$;

$V = {x^2}h = 4 Rightarrow h = 4/{x^2}left( 2 right)$.

Từ (1) và (2), ta có $Sleft( x right) = {x^2} + frac{{16}}{x}$.

$Sleft( x right) = {x^2} + frac{{16}}{x}$

$S’left( x right) = 2x – frac{{16}}{{{x^2}}} = frac{{2{x^3} – 16}}{{{x^2}}}$

$S’left( x right) = 0 Leftrightarrow x = 2$

Dựa vào $BBT$, ta có $Sleft( x right)$ đạt GTNN khi $x = 2$.

Câu 15:Giám đốc một nhà hát $A$ đang phân vân trong việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là 20 USD/người thì trung bình có 1000 người đến xem. Nhưng nếu tăng thêm 1 USD/người thì sẽ mất 100 khách hàng hoặc giảm đi 1 USD/người thì sẽ có thêm 100 khách hàng trong số trung bình. Biết rằng, trung bình, mỗi khách hàng còn đem lại 2 USD lợi nhuận cho nhà hát trong các dịch vụ đi kèm. Hãy giúp giám đốc nhà hát này xác định xem cần tính giá vé vào cửa là bao nhiêu để thu nhập là lớn nhất?

Lời giải

Trả lời: 14

Gọi giá vé sau khi điều chỉnh là $20 + x,,,,(x + 20 > 0)$

Số khách là: $1000 – 100x$

Tổng thu nhập

$fleft( x right) = left( {20 + x.1 + 2} right)left( {1000 – 100x} right)$ $ = left( {22 + x} right)left( {1000 – 100x} right)$

$ = – 100{x^2} – 1200x + 22000$

Bảng biến thiên

Suy ra giá vé là: $x + 20 = 20 – 6 = 14$ USD

Câu 16: Một người bán buôn Thanh Long Đỏ ở Lập Thạch – Vĩnh Phúc nhận thấy rằng: Nếu bán với giá 20000 nghìn $/kg$ thì mỗi tuần có 90 khách đến mua và mỗi khách mua trung bình $60;kg$. Cứ tăng giá 2000 nghìn $/kg$ thì khách mua hàng tuần giàm đi 1 và khi đó khách lại mua ít hơn mức trung bình $5;kg$, và như vậy cứ giảm giá 2000 nghìn $kg$ thì số khách mua hàng tuần tăng thêm 1 và khi đó khách lại mua nhiều hơnmức trung bình $5;kg$. Hỏi người đó phải bán với giá mỗi $kg$ là bao nhiêu để lợi nhuận thu được hàng tuần là lớn nhất, biết rằng người đó phải nộp tổng các loại thuế là 2200 nghìn $/kg$

Lời giải

Trả lời: 22000

Gọi $2000x$ nghìn $/kg$ là mức giá thay đổi tăng hoặc giảm so với giá bán bình quân.

Giá bán sau khi thay đổi là $20000 + 2000x$ nghìn $/kg$.

Số lượng người mua sau khi thay đổi giá là $90 – x$.

Khối lượng khách mua trung bình sau khi giảm giá là $60 – 5x;kg$.

Số tiền thuế phải nộp sau khi thay đổi giá: $2200left( {90 – x} right)left( {60 – 5x} right)$.

Số tiền thu được sau khi thay đổi giá là

$Tleft( x right) = left( {90 – x} right)left( {60 – 5x} right)left( {20000 + 2000x} right)$$ – 2200left( {90 – x} right)left( {60 – 5x} right)$

$ = left( {17800 + 2000x} right)left( {90 – x} right)left( {60 – 5x} right)$

$ = left( {10{x^3} – 931{x^2} + 1722x + 96120} right).1000$.

Điều kiện $left{ {begin{array}{*{20}{l}}
{x leqslant 90} \
{x leqslant 12} \
{x geqslant 8,9}
end{array} Leftrightarrow 8,9 leqslant x leqslant 12} right.$.

Ta có $T’left( x right) = left( {30{x^2} – 1862x + 1722} right) cdot 1000$.

$T’left( x right) = 0 Leftrightarrow 15{x^2} – 931x + 861 = 0 Rightarrow left[ {begin{array}{*{20}{l}}
{x approx 0,94left( N right)} \
{x approx 61,13left( L right)}
end{array}} right.$.

$Tleft( {frac{{89}}{{10}}} right) = Tleft( {12} right) = 0,Tleft( {0,94} right) = 96924000$

Do đó $x approx 1$ thì lợi nhuận cao nhất.

Do đó giá bán tốt nhất là 22000 nghìn $/kg$.

Câu 17:Cho hình thang cân có độ dài đáy nhỏ và hai cạnh bên đều bằng 1 mét. Khi đó hình thang đã cho có diện tích lớn nhất bằng?

Lời giải

Trả lời: $frac{{3sqrt 3 }}{4}$

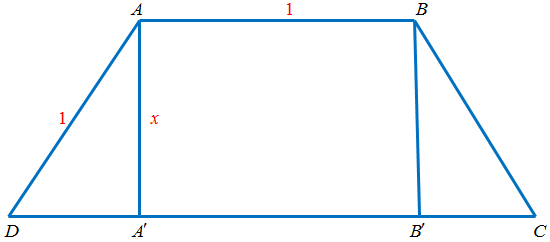
Gọi $x$ là độ dài đường cao suy ra $0 < x leqslant 1$.

Tính được đáy lớn bằng $1 + 2sqrt {1 – {x^2}} $.

Diện tích hình thang $S = left( {1 + sqrt {1 – {x^2}} } right)x$.

Xẻt hàm số $fleft( x right) = left( {1 + sqrt {1 – {x^2}} } right)x$ trên $left( {0;1} right]$.

Ta có: $f’left( x right) = frac{{ – 2{x^2} + 1 + sqrt {1 – {x^2}} }}{{sqrt {1 – {x^2}} }}$

$f’left( x right) = 0 Leftrightarrow x = frac{{sqrt 3 }}{2}$.

Lập bảng biến thiên.

Suy ra $mathop {max}limits_{left( {0;1} right]} fleft( x right) = fleft( {frac{{sqrt 3 }}{2}} right) = frac{{3sqrt 3 }}{4}$.

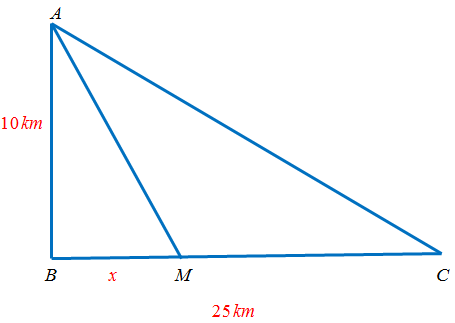
Câu 18:Nhà của ba bạn $A,B,C$ nằm ở ba vị trí tạo thành một tam giác vuông tại $B$ như hình vẽ, biết $AB = 10;km,BC = 25;km$ và ba bạn tổ chức họp mặt tại nhà bạn $C$. Bạn $B$ hẹn chở bạn $A$ tại vị trí $M$ trên đoạn đường $BC$. Giả sử luôn có xe buýt đi thẳng từ $A$ đến $M$. Từ nhà bạn $A$ đi xe buýt thẳng đến điểm hẹn $M$ với tốc độ $30;km/h$ và từ $M$ hai bạn $A,B$ di chuyển đến nhà bạn $C$ theo đoạn đường $MC$ bằng xe máy với vận tốc $50;km/h$. Hỏi $5MB + 3MC$ bằng bao nhiêu km để bạn $A$ đến nhà bạn $C$ nhanh nhất?

Lời giải

Trả lời: $frac{{3sqrt 3 }}{4}$

Đặt $BM = x,0 < x < 25$.

Ta có: $AM = sqrt {100 + {x^2}} ;MC = 25 – x$.

Thời gian bạn $A$ đi từ nhà đến nhà bạn $C$ là: $T = frac{{sqrt {100 + {x^2}} }}{{30}} + frac{{left( {25 – x} right)}}{{50}}$.

Xét hàm số $fleft( x right) = frac{{sqrt {100 + {x^2}} }}{{30}} + frac{{left( {25 – x} right)}}{{50}}$, với $0 < x < 25$.

Ta có $f’left( x right) = frac{1}{{30}}frac{x}{{sqrt {100 + {x^2}} }} – frac{1}{{50}}$.

$f’left( x right) = 0 Leftrightarrow x = frac{{15}}{2}$.

Lập bảng biến thiên

Dựa vào bảng biến thiên ta thấy $fleft( x right)$ đạt giá trị nhò nhất tại $x = frac{{15}}{2}$.

Do đó $5MB + 3MC = 5 cdot frac{{15}}{2} + 3 cdot frac{{35}}{2} = 90$.

Câu 19: Một công ty muốn làm một đường ống dẫn dầu từ một kho $A$ ở trên bờ biển đến một vị trí $B$ trên một hòn đảo. Hòn đảo cách bờ biển $6;km$. Gọi $C$ là điểm trên bờ sao cho $BC$ vuông góc với bờ biển. Khoảng cách từ $A$ đến $C$ là $9;km$. Người ta cần xác định một ví trí $D$ trên $AC$ để lắp ống dẫn theo đường gấp khúc $ADB$. Tính khoảng cách $AD$ để số tiền chi phí thấp nhất, biết rằng giá để lắp đặt mỗi $km$ đường ống trên bờ là 100.000 .000 đồng và dưới nước là 260.000 .000 đồng

Lời giải

Trả lời: 6,5

Đặt $AD = x;km,x > 0.CD = 9 – x;BD = sqrt {36 + {{(9 – x)}^2}} $

Giá thành lắp đặt là: $100 cdot {10^6}x + sqrt {36 + {{(9 – x)}^2}} cdot 260 cdot {10^6}$$ = {10^7}left[ {10x + 26sqrt {36 + {{(9 – x)}^2}} } right]$

Xét hàm số $fleft( x right) = 10x + sqrt {36 + {{(9 – x)}^2}} cdot 26;(0 < x < 9)$

$f’left( x right) = 10 – 26 cdot frac{{9 – x}}{{sqrt {36 + {{(9 – x)}^2}} }} = 0$$ Leftrightarrow 10sqrt {36 + {{(9 – x)}^2}} – 26left( {9 – x} right) = 0$

$ Leftrightarrow left{ {begin{array}{*{20}{l}}
{x leqslant 9} \
{ – 576{x^2} + 10368x – 43056 = 0}
end{array}} right.$$ Leftrightarrow x = frac{{13}}{2}$.

Lập bảng biến thiên của hàm số $fleft( x right)$ trên $left( {0;9} right)$ ta thấy hàm số đạy giá trị nhỏ nhất khi $x = frac{{13}}{2}$.

Vậy $AD = 6.5;km$.

Câu 20:Một sợi dây kim loại dài $60;cm$ được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh $a$, đoạn dây thứ hai uốn thành đường tròn đường kính $r$. Để tổng diện tích của hình vuông và hình tròn là nhỏ nhất thì tỉ số $frac{a}{r}$ là?.

Lời giải

Trả lời: 2

Độ dài đoạn dây bằng $60;cm$, cạnh hình vuông bằng $a$, bán kính đường tròn bằng $r$ nên ta có:

$4a + 2pi r = 60 Leftrightarrow r = frac{{30 – 2a}}{pi }left( 1 right)$

Gọi $S$ là tổng diện tích của hình vuông và hình tròn, suy ra $S = {a^2} + pi {r^2}left( 2 right)$.

Thay (1) vào (2) ta được $S = {a^2} + frac{{{{(30 – 2a)}^2}}}{pi }$.

Khi đó $S’ = 2a – frac{{4left( {30 – 2a} right)}}{pi } = frac{{left( {2pi + 8} right)a – 120}}{{pi = 11}}$.

Cho $S’ = 0 Leftrightarrow a = frac{{60}}{{pi + 4}}$.

Bảng biến thiên.

Dựa vào bảng biến thiên ta thấy $S$ nhỏ nhất khi $a = frac{{60}}{{pi + 4}} Rightarrow r = frac{{30}}{{pi + 4}}$.

Vậy $frac{a}{r} = 2$.