20 Câu Trắc Nghiệm Đúng Sai Tính Đơn Điệu Và Cực Trị Của Hàm Số Giải Chi Tiết

 

20 Câu Trắc Nghiệm Đúng Sai Tính Đơn Điệu Và Cực Trị Của Hàm Số Giải Chi Tiết

20 Câu trắc nghiệm đúng sai tính đơn điệu và cực trị của hàm số giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

Câu 1:Cho hàm số $y = f(x)$ có bảng biến thiên như sau

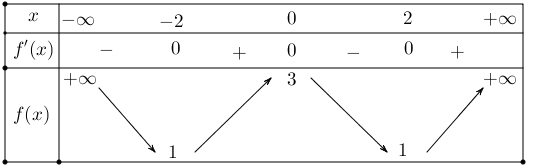
a) Hàm số nghịch biến trên khoảng $left( { – infty ; – 2} right)$.

b) Hàm số đồng biến trên khoảng $left( { – 2;0} right)$

c) Hàm số đồng biến trên khoảng $left( { – infty ;0} right)$

d) Hàm số nghịch biến trên khoảng $left( {0;2} right)$

Lời giải

a) Đ

b) Đ

c) S

d) Đ

Câu 2:Cho hàm số $y = fleft( x right)$ xác định trên $mathbb{R}$ và có bảng biến thiên như hình vẽ sau:

a) Hàm số $y = fleft( x right)$ đạt cực tiểu tại $x = 3$.

b) Hàm số $y = fleft( x right)$ đạt cực tiểu tại $x = 8$.

c) Giá trị cực đại của hàm số $y = fleft( x right)$ bằng $ – 4$.

d) Giá trị cực đại của hàm số $y = fleft( x right)$ bằng $ – 14$

Lời giải

a) S

b) Đ

c) Đ

d) S

Câu 3:Cho hàm số $y = fleft( x right)$ liên tục và xác định trên $mathbb{R}$có đồ thị đạo hàm $f’left( x right)$ là hàm số bậc ba như hình vẽ. Hàm số $y = fleft( x right)$ nghịch biến trên khoảng nào sau đây?

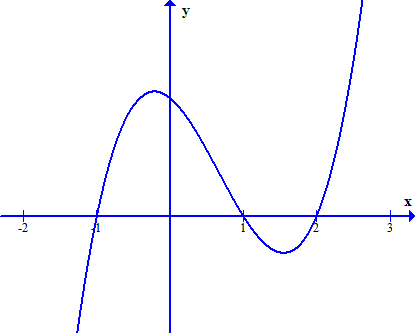
a) Hàm số nghịch biến trên khoảng $left( { – infty ; – 1} right)$.

b) Hàm số đồng biến trên khoảng $left( { – 1;1} right)$.

c) Hàm số nghịch biến trên khoảng $left( {0;1} right)$.

d) Hàm số đồng biến trên khoảng $left( {2; + infty } right)$.

Lời giải

a) Đ

b) Đ

c) S

d) Đ

Phương pháp

+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0$ nên hàm số $y = f(x)$ đồng biến trên khoảng $(a;b)$.

+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía dưới trục hoành thì $f'(x) < 0$ nên hàm số $y = f(x)$ nghịch biến trên khoảng $(a;b)$.

+ Nếu đồ thị hàm số $y = f'(x)$ cắt trục hoành tại điểm ${x_0}$ thì $f'({x_0}) = 0$.

Câu 4:Cho hàm số $fleft( x right)$ có đạo hàm là $f’left( x right) = left( {x + 4} right)left( {x + 3} right),,,forall x in mathbb{R}$.

a) Hàm số nghịch biến trên khoảng $left( { – 4; – 3} right)$.

b) Hàm số đồng biến trên khoảng $left( { – infty ; – 5} right)$.

c) Hàm số nghịch biến trên khoảng $left( {0;1} right)$.

d) Hàm số đồng biến trên khoảng $left( { – 3; + infty } right)$.

Lời giải

a) Đ

b) Đ

c) S

d) Đ

Lời giải:

Ta có:

$f'(x) = 0 Leftrightarrow left( {x + 4} right)left( {x + 3} right) = 0$

$ Leftrightarrow left[ begin{gathered}
x + 4 = 0 hfill \
x + 3 = 0 hfill \
end{gathered} right. Leftrightarrow left[ begin{gathered}
x = – 4 hfill \
x = – 3 hfill \
end{gathered} right.$

Bảng xét dấu $f'(x)$

Câu 5: Cho hàm số $gleft( x right)$ có đạo hàm $g’left( x right) = left( {{x^2} – 1} right)left( {x + 4} right)$ với mọi $x in mathbb{R}$.

a) Hàm số $y = gleft( x right)$ đạt cực đại tại $x = – 4$.

b) Hàm số $y = gleft( x right)$ đạt cực đại tại $x = – 1$.

c) Giá trị cực tiểu của hàm số $y = gleft( x right)$ bằng $g(1)$.

d) Giá trị cực tiểu của hàm số $y = gleft( x right)$ bằng $g( – 1)$

Lời giải:

a) S

b) Đ

c) Đ

d) S

$g’left( x right) = 0 Leftrightarrow left( {{x^2} – 1} right)left( {x + 4} right) = 0 Leftrightarrow left[ begin{gathered}
x = 1 hfill \
x = – 1 hfill \
x = – 4 hfill \
end{gathered} right.$

Bảng biến thiên

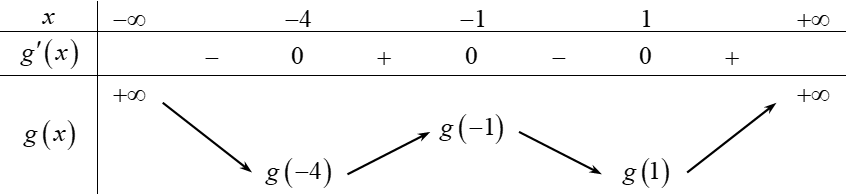
Câu 6:Cho hàm số $y = fleft( x right)$ có bảng xét dấu đạo hàm như sau

a) Hàm số nghịch biến trên khoảng $left( { – infty ; – 2} right)$.

b) Hàm số đồng biến trên khoảng $left( { – 2;0} right)$

c) Hàm số đồng biến trên khoảng $left( { – infty ;0} right)$

d) Hàm số nghịch biến trên khoảng $left( {0;2} right)$

Lời giải

a) S

b) S

c) S

d) Đ

Theo bảng xét dấu thì $y’ < 0$ khi $x in left( {0;2} right)$ nên hàm số nghịch biến trên khoảng $left( {0;2} right)$.

Câu 7:Cho hàm số $y = – frac{1}{3}{x^3} + {x^2} – x + 1$.

a) Hàm số nghịch biến trên $mathbb{R}$.

b) Hàm số đồng biến trên $mathbb{R}$.

c) Hàm số đồng biến trên $left( {1; + infty } right)$ và nghịch biến trên $left( { – infty ;1} right)$.

d) Hàm số đồng biến trên $left( { – infty ;1} right)$ và nghịch biến trên $left( {1; + infty } right)$.

Lời giải

a) Đ

b) S

c) S

d) S

$y’ = – {x^2} + 2x – 1 = – {(x – 1)^2} leqslant 0,forall x in mathbb{R}$ nên hàm số nghịch biến trên $mathbb{R}$.

Câu 8:Cho hàm số $y = frac{{x + 3}}{{x + 2}}$.

a) Hàm số nghịch biến trên $mathbb{R} setminus left{ { – 2} right}$.

b) Hàm số nghịch biến trên $left( { – infty ; – 2} right)$ và $left( { – 2; + infty } right)$.

c) Hàm số đồng biến trên $mathbb{R}$.

d) Hàm số đồng biến trên $left( { – 4; – 3} right)$.

Lời giải

a) S

b)

c) S

d) Đ

$y’ = frac{{ – 1}}{{{{(x + 2)}^2}}}$

$y’ = frac{{ – 1}}{{{{(x + 2)}^2}}} < 0;forall x in left( { – infty ; – 2} right);$

$y’ = frac{{ – 1}}{{{{(x + 2)}^2}}} < 0;forall x in left( { – 2; + infty } right)$

Câu 9: Cho hàm số $y = fleft( x right)$. Đồ thị của hàm số $y = f’left( x right)$ như hình bên. Đặt $gleft( x right) = fleft( x right) – x$. Mệnh đề nào dưới đây đúng?

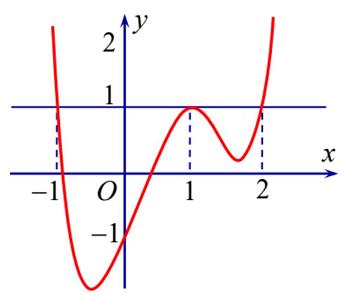
a) $gleft( 1 right) < gleft( { – 1} right) < gleft( 2 right)$.

b) $gleft( { – 1} right) < gleft( 1 right) < gleft( 2 right)$.

c) $gleft( 2 right) < gleft( 1 right) < gleft( { – 1} right)$.

d) $gleft( 2 right) < gleft( { – 1} right) < gleft( 1 right)$.

Lời giải

a) S

b) S

c) Đ

d) S

Xét hàm số $gleft( x right) = fleft( x right) – x, Rightarrow g’left( x right) = f’left( x right) – 1$.

$g’left( x right) = 0 Leftrightarrow f’left( x right) = 1 Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = – 1} \
{x = 1} \
{x = 2}
end{array}} right.$

Bảng biến thiên

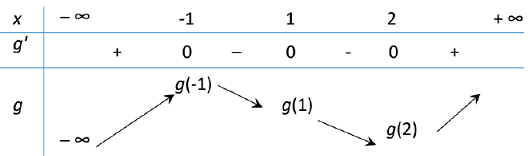
Vậy $gleft( 2 right) < gleft( 1 right) < gleft( { – 1} right)$.

Câu 10:Cho hàm số $y = frac{{{x^2} + 2x – 3}}{{x + 1}}$.

a) Hàm số đồng biến trên khoảng $left( {2;4} right)$.

b) Hàm số nghịch biến trên khoảng $left( { – infty ; + infty } right)$.

c) Hàm số nghịch biến trên các khoảng $left( { – infty ; – 1} right)$ và $left( { – 1; + infty } right)$.

d) Hàm số đồng biến trên khoảng $left( { – infty ; – 1} right)$

Lời giải

a) Đ

b) S

C.S

d) Đ

ТХĐ: $D = R setminus left{ { – 1} right}$.

$y’ = frac{{{x^2} + 2x + 5}}{{{{(x + 1)}^2}}} > 0,;forall x ne – 1$.

Suy ra Hàm số đồng biến trên các khoảng $left( { – infty ; – 1} right)$ và $left( { – 1; + infty } right)$.

Do đó đồng biến trên khoảng $left( {2;4} right)$.

Câu 11:Cho hàm số $y = {x^3} – b{x^2} – cx + 2025$ với $b,c in mathbb{R}$.

a) Hàm số luôn có 2 điểm cực trị $forall c in mathbb{R}$.

b) Hàm số luôn có 2 điểm cực trị $forall c in left( { – infty ;0} right)$.

c) Hàm số luôn có 2 điểm cực trị $forall c in left( {0; + infty } right)$.

d) Hàm số luôn có 2 điểm cực trị $forall c in mathbb{Z}$.

Lời giải

a) S

b) S

c) Đ

d) S

$y = {x^3} – {x^2} – cx + 2025$ có tập xác định là: $D = mathbb{R}$

$y’ = 3{x^2} – 2bx – c;Delta ‘ = {b^2} + 3c$.

Hàm số có hai điểm cực trị $ Leftrightarrow $ phương trình $y’ = 0$ có hai nghiệm phân biệt

$ Leftrightarrow $$Delta ‘ = {b^2} + 3c > 0$

a) Hàm số luôn có 2 điểm cực trị $forall c in mathbb{R}$ Sai.

Ta chọn $b = 0,,c = – 1 Rightarrow Delta ‘ = – 3 < 0$

b) Hàm số luôn có 2 điểm cực trị $forall c in left( { – infty ;0} right)$ Sai.

Ta chọn $b = 0,,c = – 1 Rightarrow Delta ‘ = – 3 < 0$

c) Hàm số luôn có 2 điểm cực trị $forall c in left( {0; + infty } right)$ Đúng

Ta có: $left{ begin{gathered}
{b^2} > 0 hfill \
c > 0 hfill \
end{gathered} right. Rightarrow Delta ‘ > 0$

d) Hàm số luôn có 2 điểm cực trị $forall c in mathbb{Z}$ Sai

Ta chọn $b = 0,,c = – 1 Rightarrow Delta ‘ = – 3 < 0$

Câu 12:Cho hàm số $y = fleft( x right)$ có bảng biến thiên như sau

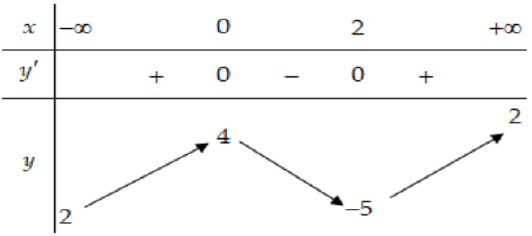
a) Hàm số đạt cực tiểu tại $x = – 5$

b) Hàm số có bốn điểm cực trị

c) Hàm số đạt cực tiểu tại $x = 2$

d) Hàm số không có cực đại

Lời giải

a) Đ

b) S

c)

d) $S$

Dựa vào bảng biến thiên. Hàm số có đạo hàm trên $mathbb{R}$ và $y’left( 2 right) = 0;y’$ đổi dấu từ âm sang dương khi đi qua $x = 2$ nên hàm số đạt cực tiểu tại $x = 2$.

Câu 13:Cho hàm số $y = frac{{{x^2} + 3}}{{x + 1}}$.

a) Cực tiểu của hàm số bằng -3

b) Cực tiểu của hàm số bằng 1

c) Cực tiểu của hàm số bằng -6

d) Cực tiểu của hàm số bằng 2

Lời giải

a) S

b) S

c) S

d) Đ

Cách 1.

Ta có: $y’ = frac{{{x^2} + 2x – 3}}{{{{(x + 1)}^2}}}$;

$y’ = 0 Leftrightarrow {x^2} + 2x – 3 = 0 Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = – 3} \
{x = 1}
end{array}} right.$

Bảng biến thiên

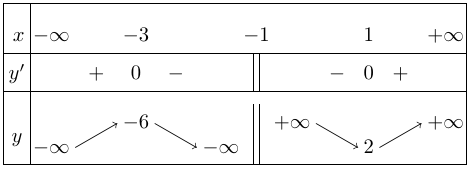
Vậy hàm số đạt cực tiểu tại $x = 1$ và giá trị cực tiểu bằng 2 .

Cách 2.

Ta có $y’ = frac{{{x^2} + 2x – 3}}{{{{(x + 1)}^2}}};$

$y’ = 0 Leftrightarrow {x^2} + 2x – 3 = 0 Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = – 3} \
{x = 1}
end{array}} right.$

$y” = frac{8}{{{{(x + 1)}^3}}}$.

Khi đó: $y”left( 1 right) = frac{1}{2} > 0;$$y”left( { – 3} right) = – frac{1}{2} < 0$.

Nên hàm số đạt cực tiểu tại $x = 1$ và giá trị cực tiểu bằng 2 .

Câu 14:Cho hàm số $y = {x^4} – 2{x^2} + 1$. Xét các mệnh đề sau đây

a) Hàm số có 3 điểm cực trị.

b) Hàm số đồng biến trên các khoảng $left( { – 1;0} right);left( {1; + infty } right)$.

c) Hàm số có 1 điểm cực trị.

d) Hàm số nghịch biến trên các khoảng $left( { – infty ; – 1} right);left( {0;1} right)$.

Lời giải

a) Đ

b) Đ

c) S

d) Đ

$y’ = 4{x^3} – 4x Rightarrow y’ = 0$

$ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0}&{ Rightarrow y = 1} \
{x = 1}&{ Rightarrow y = 0} \
{x = – 1}&{ Rightarrow y = 0}
end{array}} right.$

Bảng xét dấu:

Hàm số có 3 điểm cực trị, đổng biến trên khoảng $left( { – 1;0} right);left( {1; + infty } right)$ và nghịch biến trên khoảng $left( { – infty ; – 1} right);left( {0;1} right)$. Vậy mệnh đề $1,2,4$ đúng.

Câu 15:Cho hàm số $y = fleft( x right)$ có bảng biến thiên như sau

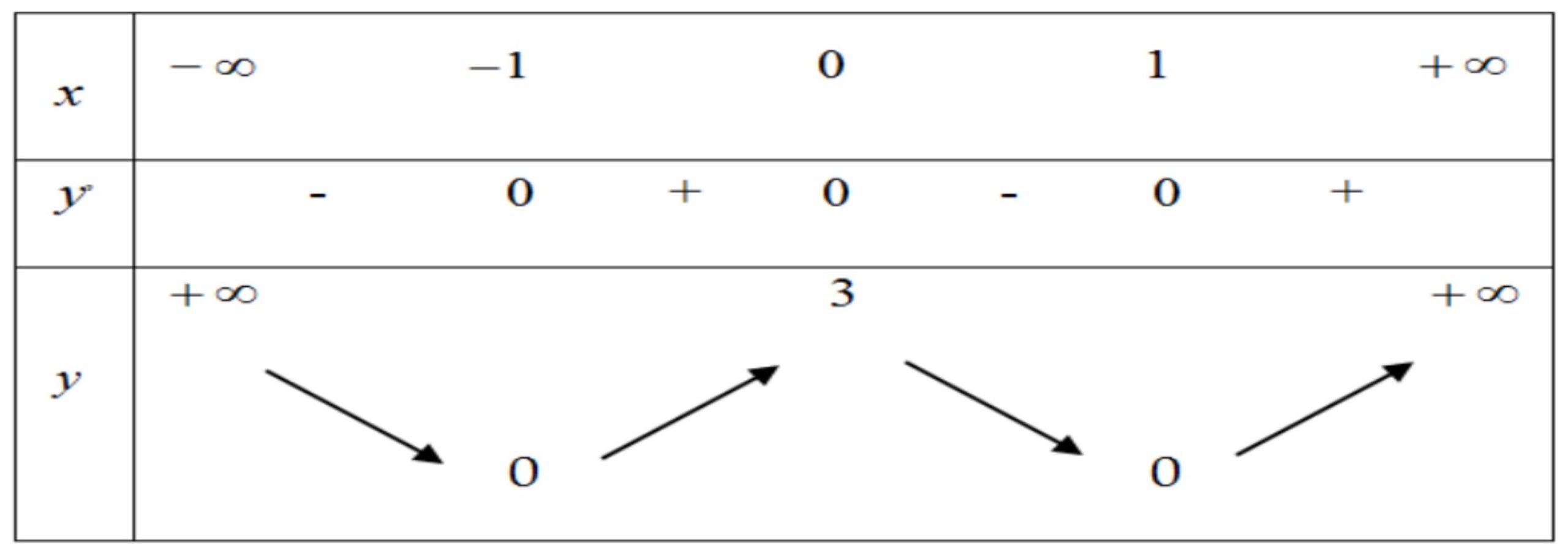
a) Hàm số có giá trị cực đại bằng 3

b) Hàm số có hai điểm cực tiểu

c) Hàm số có giá trị cực đại bằng 0

d) Hàm số có ba điểm cực trị

Lời giải

a) Đ

b) Đ

c) S

d) Đ

Câu 16:Cho hàm số $y = fleft( x right)$ có đạo hàm $f’left( x right) = {(x + 1)^2}left( {1 – x} right)left( {x + 3} right)$. Xét tính đúng sai của các mệnh đề sau?

a) Hàm số đạt cực đại tại $x = 1$

b) Giá trị cực tiểu của hàm số là $fleft( { – 3} right)$

c) Hàm số nghịch biến trên khoảng $left( { – 3;1} right)$

d) Hàm số đồng biến trên khoảng $left( { – 3;1} right)$

Lời giải

a) Đ

b) Đ

c) S

d) Đ

Ta có bảng biến thiên của hàm số $y = fleft( x right)$ như sau:

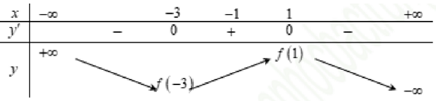
Do đó:

a) Hàm số đạt cực đại tại $x = 1$ là mệnh đề đúng

b) Giá trị cực tiểu của hàm số là $fleft( { – 3} right)$ là mệnh đề đúng

c) Hàm số nghịch biến trên khoảng $left( { – 3;1} right)$ là mệnh đề sai

d) Hàm số đồng biến trên khoảng $left( { – 3;1} right)$ là mệnh đề đúng

Câu 17:Hàm số $fleft( x right)$ có đạo hàm trên $mathbb{R}$ là hàm số $f’left( x right)$. Biết đồ thị hàm số $f’left( x right)$ được cho như hình vẽ.

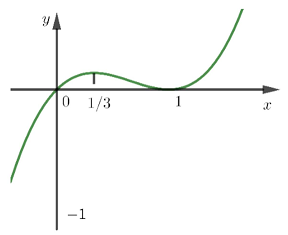
Xét tính đúng sai của các mệnh đề sau?

a) Hàm số đạt cực tiểu tại $x = 0$

b) Giá trị cực đại của hàm số là $fleft( 1 right)$

c) Hàm số nghịch biến trên khoảng $left( {0;1} right)$

d) Hàm số đồng biến trên khoảng $left( { – infty ;1} right)$

Lời giải

a) Đ

b) Đ

c) S

d) S

Ta có bảng biến thiên của hàm số $fleft( x right)$ :

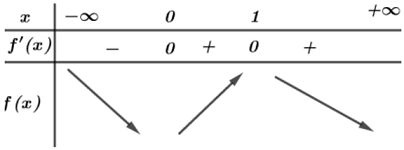
Từ bảng biến thiên ta thấy

a) Hàm số đạt cực tiểu tại $x = 0$ là mệnh đề đúng

b) Giá trị cực đại của hàm số là $fleft( 1 right)$ là mệnh đề đúng

c) Hàm số nghịch biến trên khoảng $left( {0;1} right)$ là mệnh đề sai

d) Hàm số đồng biến trên khoảng $left( { – infty ;1} right)$ là mệnh đề sai

Câu 18: Cho hàm số $y = sqrt {8 + 2x – {x^2}} $. Xét tính đúng sai của các mệnh đề sau?

a) Tập xác định của hàm số là $D = left[ { – 2;4} right]$

b) Hàm số có $y’ = frac{{1 – x}}{{sqrt {8 + 2x – {x^2}} }}$

c) Hàm số nghịch biến trên khoảng $left( {1;4} right)$

d) Giá trị cực đại của hàm số là 0

Lời giải

a) Đ

b) Đ

c) Đ

d) S

Xét hàm số: $y = sqrt {8 + 2x – {x^2}} $ có:

a) TXĐ: $D = left[ { – 2;4} right]$ là mệnh đề đúng

b) Ta có $y’ = frac{{{{left( {8 + 2x – {x^2}} right)}’}}}{{2sqrt {8 + 2x – {x^2}} }} = frac{{2 – 2x}}{{2sqrt {8 + 2x – {x^2}} }} = frac{{1 – x}}{{sqrt {8 + 2x – {x^2}} }}$ là mệnh đề đúng

c) Ta có $y’ = 0 Leftrightarrow x = 1$.

Ta có bảng biến thiên:

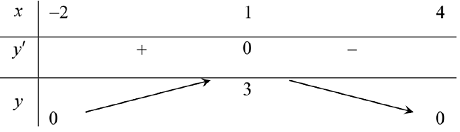
Dựa vào bảng biến thiên ta thấy

c) Hàm số nghịch biến trên khoảng $left( {1;4} right)$ là mệnh đề đúng

d) Giá trị cực đại của hàm số là 0 là mệnh đề sai

Câu 19: Cho hàm số $y = frac{{2x – m}}{{x – 1}}$. Xét tính đúng sai của các mệnh đề

a) Tập xác định của hàm số là $D = mathbb{R} setminus left{ 1 right}$

b) Khi $m = 0$ thì đồ thị hàm số cắt trục $Ox$ tại điểm $x = 1$

c) Khi $m = – 1$ thì $y’ = frac{{ – 3}}{{{{(x – 1)}^2}}}$

d) Hàm số đồng biến trên khoảng xác định của nó khi $m > 2$

Lời giải

a) Đ

b) Đ

c) Đ

d) $S$

a) là mệnh đề đúng

b) Khi $m = 0$ thì $y = frac{{2x}}{{x – 1}}$.

Do đó đồ thị hàm số cắt trục $Ox$ tại điểm $x = 0$.

Do đó mệnh đề B là sai

c) Khi $m = – 1$ thì $y = frac{{2x + 1}}{{x – 1}}$. Khi đó $y’ = frac{{ – 3}}{{{{(x – 1)}^2}}}$ là mệnh đề đúng

d) Ta có: $y’ = frac{{m – 2}}{{{{(x – 1)}^2}}}$.

Để hàm số đồng biến trên khoảng xác định của nó thì $y’ > 0 Leftrightarrow frac{{m – 2}}{{{{(x – 1)}^2}}} > 0;forall x in D Leftrightarrow m > 2$ suy ra $m in left( {2; + infty } right)$.

Do đó Mệnh đề D đúng.

Câu 20:Cho hàm số $y = frac{{cosx – 2}}{{cosx – m}}$. Xét tính đúng sai của các mệnh đề sau?

a) Đồ thị hàm số đã cho không cắt trục $Ox$.

b) Đặt $t = cosx$ thì $0 < t < 1$

c) Khi $y = 1$ thì $m = 2$

d) Hàm số nghịch biến trên khoảng $left( {0;frac{pi }{2}} right)$ khi $m > 2$

Lời giải

a) Đ

b) Đ

c) S

d) S

a) Đồ thị hàm số đã cho không cắt trục $Ox$ là mệnh đề đúng

Vì $cosx – 2 ne 0,forall x in mathbb{R}$

b) Đặt $t = cosx$, với $x in left( {0;frac{pi }{2}} right) Rightarrow 0 < t < 1$ là mệnh đề đúng

c) Khi $y = 1$ thì $m = 1$

d) Hàm số nghịch biến trên khoảng $left( {0;frac{pi }{2}} right)$ khi $m > 2$

Đặt $t = cosx,0 < t < 1$ ta có hàm số: $y = frac{{t – 2}}{{t – m}}left( 2 right),0 < t < 1 Rightarrow y’ = frac{{ – m + 2}}{{{{(t – m)}^2}}}$.

Để hàm số ban đầu nghịch biến trên khoảng $left( {0;frac{pi }{2}} right)$ thì hàm số (2) phải nghịch biến trên khoảng $(0;1)$ do đó: $left{ {begin{array}{*{20}{l}}
{ – m + 2 < 0} \
{left[ {begin{array}{*{20}{l}}
{m geqslant 1} \
{m leqslant 0}
end{array}} right.}
end{array}} right.$$ Leftrightarrow left{ {begin{array}{*{20}{l}}
{m > 2} \
{left[ {begin{array}{*{20}{l}}
{m geqslant 1} \
{m leqslant 0}
end{array}} right.}
end{array}} right. Leftrightarrow m > 2$.