Đề kiểm tra học kỳ 2 Toán 10 Cánh diều cấu trúc mới giải chi tiết-Đề 5 được soạn dưới dạng file word và PDF gồm 3 trang. Các bạn xem và tải về ở dưới.
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thi sinh chỉ chọn một phương án đúng nhất.

Câu 1.Hội đồng quản trị của công ty $X$ gồm 10 người. Hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí, biết khả năng trúng cử của mỗi người là như nhau?

A. 728 . B. 723 . C. 720 . D. 722 .

Câu 2. Tính giá trị của tổng $S = C_6^0 + C_6^1 + .. + C_6^6$ bằng:

A. 64 . B. 48 . C. 72 . D. 100 .

Câu 3.Gọi $x$ là cạnh huyền của một tam giác vuông với hai cạnh góc vuông là 1 và 3 . Mệnh đề nào sau đây là sai?

A. 3,162 là một số gần đúng của $x$. B. $sqrt {10} $ là số đúng của $x$.

C. 3,16227 766 là số đúng của $x$. D. Có vô số các số gần đúng của $x$.

Câu 4. Nếu phương sai của mẫu số liệu là $sqrt 2 $ thì độ lệch chuẩn là:

A. $sqrt 2 $. B. 2 . C. $sqrt[4]{2}$. D. $frac{1}{{sqrt 2 }}$.

Câu 5. Cho mẫu số liệu: 13 23 24 11 28 31 33 29 16. Khoảng biến thiên và khoảng tứ

phân vị của mẫu số liệu lần lượt là

A. $24;14,5$. B. $24;15,5$. C. $22;15,5$. D. $22;14,5$.

Câu 6.Một hộp đựng 10 thẻ, đánh số từ 1 đến 10. Chọn ngẫu nhiên 3 thẻ. Gọi $A$ là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8 . Số phần tử của biến cố $A$ là:

A. 2 . B. 3 . C. 4 . D. 5 .

Câu 7. Một bình đựng 4 quả cầu xanh và 6 quả cầu trắng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu toàn màu xanh là:

A. $frac{1}{{20}}$. B. $frac{1}{{30}}$. C. $frac{1}{{15}}$. D. $frac{3}{{10}}$.

Câu 8.Trong mặt phẳng tọa độ $Oxy$ cho $Aleft( {5;2} right),Bleft( {10;8} right)$. Tọa độ của vectơ $overrightarrow {AB} $ là:

A. $left( {2;4} right)$. B. $left( {5;6} right)$. C. $left( {15;10} right)$. D. $left( {50;6} right)$.

Câu 9. Phương trình đường thẳng đi qua $Bleft( {2;1} right)$ và vuông góc với $x – 2y + 1 = 0$ là:

A. $2x + y – 5 = 0$ B. $2x – y + 1 = 0$ C. $3x + 2y – 1 = 0$ D. $5x + 6y – 1 = 0$

Câu 10. Khoảng cách từ điểm $Mleft( {2;0} right)$ đến đường thẳng $Delta :left{ {begin{array}{*{20}{l}}
{x = 1 + 3t} \
{y = – 2 + 4t}
end{array}} right.$ là:

A. $frac{2}{5}$. B. $frac{{10}}{{sqrt 5 }}$. C. $frac{{sqrt 5 }}{2}$. D. $sqrt 2 $.

Câu 11.Đường tròn tâm $Ileft( {3; – 1} right)$ và bán kính $R = 2$ có phương trình là:

A. ${(x + 3)^2} + {(y – 1)^2} = 4$. B. ${(x – 3)^2} + {(y – 1)^2} = 4$. C. ${(x – 3)^2} + {(y + 1)^2} = 4$. D. ${(x + 3)^2} + {(y + 1)^2} = 4$.

Câu 12.Đường hyperbol với phương trình chính tắc $frac{{{x^2}}}{{20}} – frac{{{y^2}}}{{16}} = 1$ có tiêu cự bằng

A. 12 . B. 2 . C. 4 . D. 6 .

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Cho elip $left( E right)$ có dạng $frac{{{x^2}}}{{{a^2}}} + frac{{{y^2}}}{{{b^2}}} = 1(a > b > 0)$, có một tiêu điểm là ${F_1}left( { – 5;0} right)$ và đi qua điểm $Pleft( {6;0} right)$. Khi đó:

a) ${a^2} = 36$

b) ${b^2} = 11$

c) Tiêu cự của elip bằng 5

d) Điểm $Cleft( {1;1} right)$ nằm bên trong elip $left( E right)$

Câu 2. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.

a) Số các kết quả có thể xảy ra của phép thử là $nleft( Omega right) = 12$

b) Xác suất của biến cố “Trong 3 thẻ lấy ra có ít nhất 1 thẻ màu đỏ” là: $frac{5}{7}$

c) Xác suất của biến cố “Trong 3 thẻ lấy ra có nhiều nhất 1 thẻ màu xanh” là: $frac{5}{7}$

d) Xác suất của biến cố “Trong 3 thẻ lấy ra tất cả đều là màu đỏ” là: $frac{1}{{12}}$

Câu 3.Cho biết tình hình thu hoạch lúa vụ mùa năm 2022 của ba hợp tác xã ở một địa phương như sau:

Hợp tác xã	Năng suất lúa (tạ/ha)	Diện tích trồng lúa (ha)
A	40	150
B	38	130
C	36	120

Khi đó:

a) Sản lượng lúa của hợp tác xã A là: 6000 (tạ).

b) Sản lượng lúa của hợp tác xã $B$ là: 4950 (tạ).

c) Sản lượng lúa của hợp tác xã $C$ là: 4120 (tạ).

d) Năng suất lúa trung bình của toàn bộ ba hợp tác xã là: 38,15 (tạ/ha).

Câu 4.Đường tròn $left( C right)$ đi qua hai điểm $Aleft( {1;2} right),Bleft( {3;4} right)$ và tiếp xúc $Delta :3x + y – 3 = 0$. Khi đó:

a) Có hai đường tròn $left( C right)$ thỏa mãn

b) Tổng đường kính của các đường tròn $left( C right)$ bằng: $2sqrt {10} $

c) Điểm $Mleft( {3;2} right)$ nằm bên trong các đường tròn $left( C right)$

d) Điểm $Nleft( {1;0} right)$ nằm trên ít nhất một đường tròn $left( C right)$

Phần 3. Câu trả lời ngắn.
Thi sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1.Có hai con tàu $A,B$ xuất phát từ hai bến, chuyển động theo đường thẳng ngoài biển. Trên màn hình ra-đa của trạm điều khiển (xem như mặt phẳng tọa độ $Oxy$ với đơn vị trên các trục tính bằng ki-lômét), tại thời điểm $t$ (giờ), vị trí của tàu $A$ có tọa độ được xác định bởi công thức $left{ {begin{array}{*{20}{l}}
{x = 3 – 33t} \
{y = – 4 + 25t}
end{array}} right.$; vị trí tàu $B$ có tọa độ là $left( {4 – 30t;3 – 40t} right)$.

Nếu tàu $A$ đứng yên ở vị trí ban đầu, tàu $B$ chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu?

Câu 2.Trong mặt phẳng tọa độ $Oxy$, cho hình thoi $ABCD$ có $AC = 2BD$ và đường tròn tiếp xúc với các cạnh của hình thoi có phương trình $left( C right):{x^2} + {y^2} = 4$. Viết phương trình chính tắc của elip $left( E right)$ đi qua các đỉnh $A,B,C,D$ của hình thoi với điểm $A$ nằm trên trục $Ox$.

Câu 3.Một người có 500 triệu đồng gửi tiết kiệm ngân hàng với lãi suất $7,2% /$ năm. Với giả thiết sau mỗi tháng người đó không rút tiền thì số tiền lãi được nhập vào số tiền ban đầu. Đây được gọi là hình thức lãi kép. Biết số tiền cả vốn lẫn lãi $T$ sau $n$ tháng được tính bởi công thức $T = {T_0}{(1 + r)^n}$, trong đó ${T_0}$ là số tiênn gửi lúc đầu và $r$ là lãi suất của một tháng. Dùng hai số hạng đầu tiên trong khai triển của nhị thức Niu – tơn, tính gần đúng số tiên người đó nhận được (cả gốc lẫn lãi) sau 6 tháng.

Câu 4.Trong một chiếc hộp có 4 viên bi đỏ, 4 viên bi xanh và 2 viên bi vàng. Lấy ra ngẫu nhiên 2 viên bi từ trong hộp. Tính xác suất để lấy ra được 2 viên bi vàng.

Câu 5. Mầu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày.

7

8

22

20

15

18

19

13

11

Tìm khoảng tứ phân vị của mẫu số liệu này

Câu 6. Cho đường tròn $left( C right)$ có phương trình ${x^2} + {y^2} – 2x + 2y – 7 = 0$ và hai điểm $Aleft( {2; – 2} right),Bleft( { – 3; – 1} right)$. Gọi $M,N$ là các điểm thuộc $left( C right)$ sao cho $AM,AN$ lần lượt đạt giá trị lớn nhất và nhỏ nhất. Tính $AM + AN$.

ĐÁP ÁN VÀ LỜI GIẢI THAM KHẢO

Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu l đến câu 12. Mối câu hỏi thí sinh chỉ chọn một phương án đúng nhất.

1C	2A	3C	4C	5C	6C
7B	8B	9A	10A	11C	12A

Câu 1. Hội đồng quản trị của công ty $X$ gồm 10 người. Hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí, biết khả năng trúng cử của mỗi người là như nhau?

A. 728 .

B. 723 .

C. 720 .

D. 722 .

Lời giải

Chọn C

Chọn một người làm chủ tịch: có 10 cách chọn. Chọn một người làm phó chủ tịch: có 9 cách. Chọn một người làm thư kí: có 8 cách.

Vậy số cách chọn thỏa mãn là: 10.9.8 =720 .

Câu 2.Tính giá trị của tổng $S = C_6^0 + C_6^1 + .. + C_6^6$ bằng:

A. 64 .

B. 48 .

C. 72 .

D. 100 .

Chọn A

Lời giải

Xét khai triển: ${(1 + x)^6} = $ $C_6^0 + C_6^1x + C_6^2{x^2} + C_6^3{x^3} + C_6^4{x^4} + C_6^5{x^5} + C_6^6{x^6}$.

Thay $x = 1$, ta được: $C_6^0 + C_6^1 + C_6^2 + C_6^3 + C_6^4 + C_6^5 + C_6^6$ $ = {(1 + 1)^6} = {2^6} = 64$.

Câu 3.Gọi $x$ là cạnh huyền của một tam giác vuông với hai cạnh góc vuông là 1 và 3 . Mệnh đề nào sau đây là sai?

A. 3,162 là một số gần đúng của $x$.

B. $sqrt {10} $ là số đúng của $x$.

C. 3,16227 766 là số đúng của $x$.

D. Có vô số các số gần đúng của $x$.

Chọn C

Lời giải

Cạnh huyền của tam giác vuông là $x = sqrt {{1^2} + {3^2}} = sqrt {10} = 3,16227766 ldots $

Vì vậy các số 3,162;3,16227766 chỉ là những số gần đúng.

Câu 4.Nếu phương sai của mẫu số liệu là $sqrt 2 $ thì độ lệch chuẩn là:

A. $sqrt 2 $.

B. 2 .

C. $sqrt[4]{2}$.

D. $frac{1}{{sqrt 2 }}$.

Chọn C

Lời giải

Câu 5. Cho mẫu số liệu: 13 23 24 11 28 31 33 29 16. Khoảng biến thiên và khoảng tứ

phân vị của mẫu số liệu lần lượt là

A. $24;14,5$.

B. $24;15,5$.

C. $22;15,5$.

D. $22;14,5$.

Chọn C

Lời giải

Giá trị lớn nhất và nhỏ nhất nhất của mẫu theo thứ tự là $33;11$ nên khoảng biến thiên là $R = 33 – 11 = 22$.

Các tứ phân vị là: ${Q_1} = 14,5;{Q_2} = 24;{Q_3} = 30$. Vì vậy khoảng tứ phân vị là $Delta Q = {Q_3} – {Q_1} = 30 – 14,5 = 15,5$

Câu 6. Một hộp đựng 10 thẻ, đánh số từ 1 đến 10. Chọn ngẫu nhiên 3 thẻ. Gọi $A$ là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8 . Số phần tử của biến cố $A$ là:

A. 2 .

B. 3 .

C. 4 .

D. 5 .

Chọn C

Lời giải

Ta có: $A = left{ {left( {1;2;3} right),left( {1;2;4} right),left( {1;2;5} right),left( {1;3;4} right)} right}$.

Câu 7.Một bình đựng 4 quả cầu xanh và 6 quả cầu trắng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu toàn màu xanh là:

A. $frac{1}{{20}}$.

B. $frac{1}{{30}}$.

C. $frac{1}{{15}}$.

D. $frac{3}{{10}}$.

Chọn B

Lời giải

$nleft( Omega right) = C_{10}^3 = 120$.

Biến cố $A$ : “Được ba quả toàn màu xanh”

$ Rightarrow nleft( A right) = C_4^3 = 4 Rightarrow pleft( A right) = frac{{nleft( A right)}}{{nleft( Omega right)}} = frac{1}{{30}}$.

Câu 8. Trong mặt phẳng tọa độ $Oxy$ cho $Aleft( {5;2} right),Bleft( {10;8} right)$. Tọa độ của vectơ $overrightarrow {AB} $ là:

A. $left( {2;4} right)$.

B. $left( {5;6} right)$.

C. $left( {15;10} right)$.

D. $left( {50;6} right)$.

Chọn B

Lời giải

Câu 9.Phương trình đường thẳng đi qua $Bleft( {2;1} right)$ và vuông góc với $x – 2y + 1 = 0$ là:

A. $2x + y – 5 = 0$

B. $2x – y + 1 = 0$

C. $3x + 2y – 1 = 0$

D. $5x + 6y – 1 = 0$

Chọn A

Lời giải

Phương trình đường thẳng vuông góc với $x – 2y + 1 = 0$ có dạng $2x + y + c = 0$ mà đường thẳng trên đi qua $Bleft( {2;1} right) Rightarrow 4 + 1 + c = 0 Rightarrow c = – 5 Rightarrow 2x + y – 5 = 0$.

Câu 10. Khoảng cách từ điểm $Mleft( {2;0} right)$ đến đường thẳng $Delta :left{ {begin{array}{*{20}{l}}
{x = 1 + 3t} \
{y = – 2 + 4t}
end{array}} right.$ là:

A. $frac{2}{5}$.

B. $frac{{10}}{{sqrt 5 }}$.

C. $frac{{sqrt 5 }}{2}$.

D. $sqrt 2 $.

Chọn A

Lời giải

Phương trình tổng quát $Delta :4x – 3y – 10 = 0$. Khi đó $dleft( {M,Delta } right) = frac{{left| {4.2 – 3.0 – 10} right|}}{{sqrt {{4^2} + {{( – 3)}^2}} }} = frac{2}{5}$.

Câu 11. Đường tròn tâm $Ileft( {3; – 1} right)$ và bán kính $R = 2$ có phương trình là:

A. ${(x + 3)^2} + {(y – 1)^2} = 4$.

B. ${(x – 3)^2} + {(y – 1)^2} = 4$.

C. ${(x – 3)^2} + {(y + 1)^2} = 4$.

D. ${(x + 3)^2} + {(y + 1)^2} = 4$.

Chọn C

Lời giải

Câu 12. Đường hyperbol với phương trình chính tắc $frac{{{x^2}}}{{20}} – frac{{{y^2}}}{{16}} = 1$ có tiêu cự bằng

A. 12.

B. 2 .

C. 4 .

D. 6 .

Chọn A

Lời giải

Ta có: $left{ {begin{array}{*{20}{l}}
{{a^2} = 20} \
{{b^2} = 16} \
{{c^2} = {a^2} + {b^2}}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{a = 2sqrt 5 } \
{b = 4} \
{c = 6}
end{array}} right.$.

Tiêu cự $2c = 12$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1.Cho elip $left( E right)$ có dạng $frac{{{x^2}}}{{{a^2}}} + frac{{{y^2}}}{{{b^2}}} = 1,(a > b > 0)$, có một tiêu điểm là ${F_1}left( { – 5;0} right)$ và đi qua điểm $Pleft( {6;0} right)$. Khi đó:

a) ${a^2} = 36$

b) ${b^2} = 11$

c) Tiêu cự của elip bằng 5

d) Điểm $Cleft( {1;1} right)$ nằm bên trong elip $left( E right)$

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Đúng

Vì elip $left( E right)$ đi qua điểm $Pleft( {6;0} right)$ nên $frac{{{6^2}}}{{{a^2}}} + frac{{{0^2}}}{{{b^2}}} = 1 Rightarrow {a^2} = 36$. Vì elip $left( E right)$ có một tiêu điểm là ${F_1}left( { – 5;0} right)$ nên $c = 5$ và ${b^2} = {a^2} – {c^2} = 36 – 25 = 11$. Vậy phương trình chính tắc của đường elip $left( E right)$ là: $frac{{{x^2}}}{{36}} + frac{{{y^2}}}{{11}} = 1$.

Câu 2.Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.

a) Số các kết quả có thể xảy ra của phép thử là $nleft( Omega right) = 12$

b) Xác suất của biến cố “Trong 3 thẻ lấy ra có ít nhất 1 thẻ màu đỏ” là: $frac{5}{7}$

c) Xác suất của biến cố “Trong 3 thẻ lấy ra có nhiều nhất 1 thẻ màu xanh” là: $frac{5}{7}$

d) Xác suất của biến cố “Trong 3 thẻ lấy ra tất cả đều là màu đỏ” là: $frac{1}{{12}}$

Đáp án

a) Đúng

b) Sai

c) Sai

d) Đúng

Lời giải

a)

Kí hiệu $X$ là thẻ xanh, thẻ là đỏ và $V$ là thẻ vàng. Các kết quả có thể xảy ra trong 3 lần lấy thẻ từ hộp có thể được mô tả bởi sơ đồ hình cây ở trên.

b) Số các kết quả có thể xảy ra của phép thử là $nleft( Omega right) = 12$ Biến cố $A$ : “Trong 3 thẻ lây ra có ít nhất 1 thẻ màu đỏ”. $nleft( A right) = 10$. Xác suất của biến cố $A:Pleft( A right) = frac{{nleft( A right)}}{{nleft( Omega right)}} = frac{5}{6}$.

c) Số các kết quả có thể xảy ra $nleft( Omega right) = 12$

Biến cố B: “Trong 3 thẻ lây ra có nhiêu nhất 1 thẻ màu xanh”. $nleft( B right) = 10$. Xác suất của biến cố

$B:Pleft( B right) = frac{{nleft( B right)}}{{nleft( Omega right)}} = frac{5}{6}$.

d) $Pleft( D right) = frac{1}{{12}}$

Câu 3. Cho biết tình hình thu hoạch lúa vụ mùa năm 2022 của ba hợp tác xã ở một địa phương như sau:

Hợp tác xã	Năng suất lúa (tạ/ha)	Diện tích trồng lúa (ha)
A	40	150
B	38	130
C	36	120

Khi đó:

a) Sản lượng lúa của hợp tác xã A là: 6000 (tạ).

b) Sản lượng lúa của hợp tác xã $B$ là: 4950 (tạ).

c) Sản lượng lúa của hợp tác xã $C$ là: 4120 (tạ).

d) Năng suất lúa trung bình của toàn bộ ba hợp tác xã là: 38,15 (tạ/ha).

Đáp án

a) Đúng

b) Sai

c) Sai

d) Đúng

Lời giải

Ta biết: Sản lượng thu được $ = ($ Năng suất $) times ($ Diện tích $)$.

Sản lượng lúa của hợp tác xã $A$ là: $40 times 150 = 6000$ (tạ).

Sản lượng lúa của hợp tác xã B là: $38 times 130 = 4940$ (tạ).

Sản lượng lúa của hợp tác xã $C$ là: $36 times 120 = 4320$ (tạ).

Tổng sản lượng lúa của ba hợp tác xã là: $6000 + 4940 + 4320 = 15260$ (tạ).

Tổng diện tích trồng của cả ba hợp tác xã là: $150 + 130 + 120 = 400left( {ha} right)$.

Năng suất lúa trung bình của toàn bộ ba hợp tác xã là: $frac{{15260}}{{400}} = 38,15$ (tạ/ha).

Câu 4. Đường tròn $left( C right)$ đi qua hai điểm $Aleft( {1;2} right),Bleft( {3;4} right)$ và tiếp xúc $Delta :3x + y – 3 = 0$. Khi đó:

a) Có hai đường tròn $left( C right)$ thỏa mãn

b) Tổng đường kính của các đường tròn $left( C right)$ bằng: $2sqrt {10} $

c) Điểm $Mleft( {3;2} right)$ nằm bên trong các đường tròn $left( C right)$

d) Điểm $Nleft( {1;0} right)$ nằm trên ít nhất một đường tròn $left( C right)$

Đáp án

a) Đúng

b) Sai

c) Đúng

d) Đúng

Lời giải

Gọi tâm đường tròn là $Ileft( {a;b} right)$, ta có: $dleft( {I,Delta } right) = frac{{left| {3a + b – 3} right|}}{{sqrt {10} }}$.

Theo giả thiết $left{ {begin{array}{*{20}{l}}
{I{A^2} = I{B^2}} \
{I{A^2} = {{(dleft( {I,Delta } right))}^2}}
end{array}} right.$

$ Leftrightarrow left{ {begin{array}{*{20}{l}}
{{{(a – 1)}^2} + {{(b – 2)}^2} = {{(a – 3)}^2} + {{(b – 4)}^2}} \
{{{(a – 1)}^2} + {{(b – 2)}^2} = frac{{{{(3a + b – 3)}^2}}}{{10}}}
end{array}} right.$

$ Leftrightarrow left{ {begin{array}{*{20}{l}}
{a + b = 5} \
{{a^2} – 2a + 9{b^2} – 34b + 41 – 6ab = 0}
end{array}} right.$

Thay (1) vào (2): ${(5 – b)^2} – 2left( {5 – b} right) + 9{b^2} – 34b + 41 – 6left( {5 – b} right)b = 0$

$ Leftrightarrow 4{b^2} – 18b + 14 = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{b = 1}&{ Rightarrow a = 4 Rightarrow R = sqrt {10} } \
{b = frac{7}{2}}&{ Rightarrow a = frac{3}{2} Rightarrow R = frac{{sqrt {10} }}{2}}
end{array}} right.$.

Vậy có hai đường tròn thỏa mãn: ${left( {x – frac{7}{2}} right)^2} + {left( {y – frac{3}{2}} right)^2} = frac{5}{2}$ và ${(x – 4)^2} + {(y – 1)^2} = 10$

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Có hai con tàu $A,B$ xuất phát từ hai bến, chuyển động theo đường thẳng ngoài biển. Trên màn hình ra-đa của trạm điều khiển (xem như mặt phẳng tọa độ $Oxy$ với đơn vị trên các trục tính bằng ki-lômét), tại thời điểm $t$ (giờ), vị trí của tàu $A$ có tọa độ được xác định bởi công thức $left{ {begin{array}{*{20}{l}}
{x = 3 – 33t} \
{y = – 4 + 25t}
end{array}} right.$; vị trí tàu $B$ có tọa độ là $left( {4 – 30t;3 – 40t} right)$.

Nếu tàu $A$ đứng yên ở vị trí ban đầu, tàu $B$ chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu? Trả lời: $3,4left( {;km} right)$

Lời giải

Khi tàu $A$ đứng yên, vị trí ban đầu của nó có tọa độ $Pleft( {3; – 4} right)$; vị trí tàu $B$ ứng với thời gian $t$ là $Qleft( {4 – 30t;3 – 40t} right)$;

$PQ = sqrt {{{(1 – 30t)}^2} + {{(7 – 40t)}^2}} = sqrt {2500{t^2} – 620t + 50} $.

Đoạn $PQ$ ngắn nhất ứng với $t = – frac{b}{{2a}} = frac{{620}}{{2.2500}} = frac{{31}}{{250}} = 0,124$ (giây).

Khi đó : $P{Q_{min}} = sqrt {2500 cdot {{(0,124)}^2} – 620 cdot left( {0,124} right) + 50} = frac{{17}}{5} = 3,4left( {;km} right)$.

Câu 2. Trong mặt phẳng tọa độ $Oxy$, cho hình thoi $ABCD$ có $AC = 2BD$ và đường tròn tiếp xúc với các cạnh của hình thoi có phương trình $left( C right):{x^2} + {y^2} = 4$. Viết phương trình chính tắc của elip $left( E right)$ đi qua các đỉnh $A,B,C,D$ của hình thoi với điểm $A$ nằm trên trục $Ox$.

Trả lời: $frac{{{x^2}}}{{20}} + frac{{{y^2}}}{5} = 1$

Lời giải

Giả sử phương trình elip $left( E right)$ là $frac{{{x^2}}}{{{a^2}}} + frac{{{y^2}}}{{{b^2}}} = 1,,(a > b > 0)$.

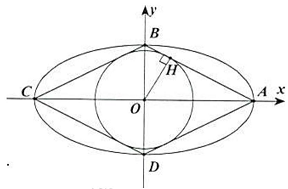
Đường tròn $left( C right):{x^2} + {y^2} = 4$ có tâm $Oleft( {0;0} right)$ và bán kính $R = 2$.

Vì $left( C right)$ tiếp xúc với các cạnh của hình thoi và $A in Ox$ nên $C in Ox$ và $B,D in Oy$.

Các điểm $A,B,C,D in left( E right)$ nên $A,B,C,D$ là các đỉnh của $left( E right)$.

$A,B in left( E right) Rightarrow Aleft( {a;0} right),Bleft( {0;b} right) Rightarrow OA = a,OB = b$.

Vì $OA = 2OB$ nên $a = 2b$.

Kẻ $OH bot ABleft( {H in AB} right)$.

Ta có $OH = R = 2$.

Tam giác $ABO$ vuông tại $O$ có $frac{1}{{O{H^2}}} = frac{1}{{O{A^2}}} + frac{1}{{O{B^2}}} Leftrightarrow frac{1}{4} = frac{1}{{{a^2}}} + frac{4}{{{a^2}}} Leftrightarrow {a^2} = 20 Rightarrow {b^2} = 5$.

Vậy phương trình $left( E right)$ là $frac{{{x^2}}}{{20}} + frac{{{y^2}}}{5} = 1$.

Câu 3. Một người có 500 triệu đồng gửi tiết kiệm ngân hàng với lãi suất $7,2% /$năm. Với giả thiết sau mỗi tháng người đó không rút tiền thì số tiền lãi được nhập vào số tiền ban đầu. Đây được gọi là hình thức lãi kép. Biết số tiền cả vốn lẫn lãi $T$ sau $n$ tháng được tính bởi công thức $T = {T_0}{(1 + r)^n}$, trong đó ${T_0}$ là số tiênn gửi lúc đầu và $r$ là lãi suất của một tháng. Dùng hai số hạng đầu tiên trong khai triển của nhị thức Niu – tơn, tính gần đúng số tiên người đó nhận được (cả gốc lẫn lãi) sau 6 tháng.

Trả lời: 518000000 đồng.

Lời giải

Lãi suất của một tháng $r = frac{{7,2}}{{12}}% = 0,6% $ / tháng.

Ta có: $T = {T_0}{(1 + r)^n}$.

Suy ra: $T = {500.10^6}{(1 + 0,006)^6}$ $ approx {500.10^6}left( {C_6^0 + C_6^1 cdot 0,006} right) approx 518000000$đồng.

Vậy: sau 6 tháng người đó nhận được hơn 518000000 đồng.

Câu 4.Trong một chiếc hộp có 4 viên bi đỏ, 4 viên bi xanh và 2 viên bi vàng. Lấy ra ngẫu nhiên 2 viên bi từ trong hộp. Tính xác suất để lấy ra được 2 viên bi vàng.

Trả lời: $frac{1}{{45}}$

Số viên bi có trong hộp là: $4 + 4 + 2 = 10$ (viên bi).

Lời giải

Lấy ra ngẫu nhiên 2 viên bi từ hộp mà không quan trọng thứ tự nên số phần tử của không gian mẫu là:

$nleft( Omega right) = C_{10}^2 = 45$.

Gọi $E$ là biến cố lấy được hai viên bi vàng. Vì chỉ có một cách lấy ra được hai viên bi vàng từ hộp nên ta có $nleft( E right) = 1$. Vậy xác suất của biến cố $E$ là: $Pleft( E right) = frac{{nleft( E right)}}{{nleft( Omega right)}} = frac{1}{{45}}$.

Câu 5. Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày.

7

8

22

20

15

18

19

13

11

Tìm khoảng tứ phân vị của mẫu số liệu này

Trả lời: 10

Lời giải

Trước hết ta sắp xếp mẫu số liệu theo thứ tự không giảm như sau

7

8

11

13

15

18

19

29

22

Mẫu số liệu này gồm 9 giá trị nên trung vị là số chính giữa ${Q_2} = 15$.

Nửa số liệu bên trái là 7;8;11;13 gồm 4 giá trị, hai phần tử chính giữa là $8;11$.

Do đó ${Q_1} = frac{{8 + 11}}{2} = 9,5$.

Nửa số liệu bên phải là 18;19;20;22 gồm 4 giá trị, hai phần tử chính giữa là 19;20 .

Do đó ${Q_3} = frac{{19 + 20}}{2} = 19,5$.

Vậy khoảng tứ phân vị của mẫu số liệu này là ${Delta _Q} = {Q_3} – {Q_1} = 10$.

Câu 6.Cho đường tròn $left( C right)$ có phương trình ${x^2} + {y^2} – 2x + 2y – 7 = 0$ và hai điểm $Aleft( {2; – 2} right),Bleft( { – 3; – 1} right)$.

Gọi $M,N$ là các điểm thuộc $left( C right)$ sao cho $AM,AN$ lần lượt đạt giá trị lớn nhất và nhỏ nhất. Tính $AM + AN$.

Trả lời: 6

(C) có tâm $Ileft( {1; – 1} right)$ và bán kính $R = sqrt {1 + 1 + 7} = 3$.

Lời giải

Ta có $:IA = sqrt {{{(2 – 1)}^2} + {{( – 2 + 1)}^2}} = sqrt 2 < R$ nên $A$ nằm bên trong đường tròn.

$IB = sqrt {{{( – 3 – 1)}^2} + {{( – 1 + 1)}^2}} = 4 > R$ nên $B$ nằm bên ngoài đường tròn.

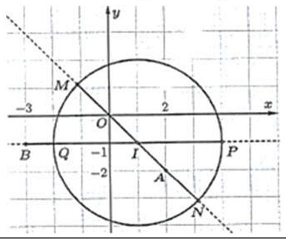
Vì $M$ thuộc $left( C right)$ và $AM$ lớn nhất nên $A,I,M$ thẳng hàng ( $I$ nằm giữa $A,M$ ) ta có: $AM = R + IA$. $N$ thuộc $left( C right),AN$ bé nhất nên $I,A,N$ thẳng hàng ( $A$ nằm giữa $I,N$ ), ta có $AN = R – IA$.

Suy ra: $AM + AN = left( {R + IA} right) + left( {R – IA} right) = 2R = 6$.