Đề Ôn Thi HK2 Toán 11 Chân Trời Sáng Tạo Cấu Trúc Mới Giải Chi Tiết-Đề 4

Đề ôn thi HK2 Toán 11 Chân trời sáng tạo cấu trúc mới giải chi tiết-Đề 4 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.

Câu 1.Trong các khẳng định sau khẳng định nào sai?

A. ${2^{30}} < {3^{20}}$. B. $0,{99^pi } > 0,{99^e}$. C. $lo{g_{{a^2} + 2}}left( {{a^2} + 1} right) geqslant 0$. D. ${4^{ – sqrt 3 }} < {4^{ – sqrt 2 }}$.

Câu 2. Đồ thị (hình bên) là đồ thị của hàm số nào ?

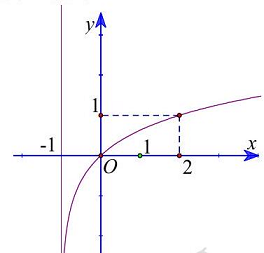
A. $y = {log_2}x + 1$. B. $y = {log_2}left( {x + 1} right)$. C. $y = {log_3}x$. D. $y = {log_3}left( {x + 1} right)$.

Câu 3.Tập nghiệm của bất phương trình $lo{g_{frac{1}{2}}}left( {{x^2} – x + 7} right) > 0$ là

A. $left( { – infty ;2} right) cup left( {3; + infty } right)$. B. $left( { – infty ;2} right)$. C. $left( {2;3} right)$. D. $left( {3; + infty } right)$.

Câu 4.Cho hình lập phương $ABCD cdot A’B’C’D’$. Góc giữa hai đường thẳng $A’C’$ và $BD$ bằng.

A. ${60^ circ }$. B. ${30^ circ }$. C. ${45^ circ }$. D. ${90^ circ }$.

Câu 5. Cho hình chóp $S cdot ABCD$ có đáy là hình vuông cạnh $a,SA bot left( {ABCD} right)$ và $SA = asqrt 3 $ Gọi $alpha $ là góc tạo bởi giữa đường thẳng $SB$ và mặt phẳng $left( {SAC} right)$, khi đó $alpha $ thỏa mãn hệ thức nào sau đây:

A. $cosalpha = frac{{sqrt 2 }}{8}$. B. $sinalpha = frac{{sqrt 2 }}{8}$. C. $sinalpha = frac{{sqrt 2 }}{4}$. D. $cosalpha = frac{{sqrt 2 }}{4}$.

Câu 6.Cho hình lập phương $ABCD cdot A’B’C’D’$. Khẳng định nào sau đây sai?

A. $mpleft( {AA’C’C} right) bot mpleft( {ABCD} right)$. B. $mpleft( {ABB’A’} right) bot mpleft( {BDD’B’} right)$.

C. $mpleft( {ABB’A’} right) bot mpleft( {A’B’C’D’} right)$. D. $mpleft( {ACC’A’} right) bot mpleft( {BB’D’D} right)$.

Câu 7. Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc nhau và $OA = OB = OC = 3a$. Tính khoảng cách giữa hai đường thẳng $AC$ và $OB$.

A. $frac{{3a}}{2}$. B. $frac{{asqrt 2 }}{2}$. C. $frac{{3asqrt 2 }}{2}$. D. $frac{{3a}}{4}$.

Câu 8.Cho hình chóp $S.ABC$ có $SA$ vuông góc mặt đáy, tam giác $ABC$ vuông tại $A,SA = 2;cm$, $AB = 4;cm,AC = 3;cm$. Tính thể tích khối chóp $S.ABC$.

A. $frac{{12}}{3};c{m^3}$. B. $frac{{24}}{5};c{m^3}$. C. $frac{{24}}{3};c{m^3}$. D. $24;c{m^3}$.

Câu 9. Nhi và Nhung thường xuyên đến cùng một quán cà phê cùng khung giờ, tuy nhiên hai bạn không đi cùng nhau. Nhi thường đến vào 2 ngày bất kỳ trong tuần, Nhung thì thường đến 3 ngày bất kỳ. Tính xác suất hai bạn gặp được nhau.

A. $P = frac{6}{{49}}$. B. $P = frac{8}{{49}}$. C. $P = frac{{15}}{{49}}$. D. $P = frac{{20}}{{49}}$.

Câu 10.Tung một đồng xu 3 lần. Xác suất đồng xu xuất hiện 2 lần mặt ngửa và một lần mặt sấp là:

A. $frac{1}{4}$. B. $frac{2}{3}$. C. $frac{3}{8}$. D. $frac{1}{2}$.

Câu 11.Tìm đạo hàm của hàm số $y = x{e^x}$

A. $1 + {e^x}$. B. $left( {1 + x} right){e^x}$. C. $left( {1 – x} right){e^x}$. D. ${e^x}$.

Câu 12.Cho hàm số $y = – 2{x^3} + 6{x^2} – 5$ có đồ thị $left( C right)$. Phương trình tiếp tuyến của $left( C right)$ tại điểm $M$ thuộc $left( C right)$ và có hoành độ bằng 3 là

A. $y = 18x – 49$. B. $y = – 18x – 49$. C. $y = – 18x + 49$. D. $y = 18x + 49$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mối ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Một hộp chứa 15 viên bi xanh và 20 viên bi đỏ, có cùng kích thước và khối lượng. Lần lượt lấy ngẫu nhiên ra 2 viên bi, mỗi lần một viên. Gọi $A$ là biến cố “Lây được viên bi màu xanh ở lần thứ nhất” và $B$ là biến cố “Lấy được viên bi màu xanh ở lần thứ hai”. Khi đó:

a) Hai biến cố $A$ và $B$ không độc lập

b) $Pleft( {AB} right) = frac{3}{{17}}$

c) $Pleft( {Aoverline B } right) = frac{{60}}{{119}}$

d) Xác suất để hai viên bi lấy ra khác màu là: $frac{{30}}{{119}}$

Câu 2. Xét khối tứ diện $ABCD$ có cạnh $AB = x$, các cạnh còn lại đều bằng $2sqrt 3 $. Các mệnh đề sau đúng hay sai?

a) Diện tích tam giác $BCD$ bằng ${S_{BCD}} = 3sqrt 3 $

b) ${V_{ABCD}} = frac{{sqrt 3 }}{3}xsqrt {36 – {x^2}} $

c) Khi $x = 3$ thì $V = frac{9}{4}$

d) Khi $x = 3sqrt 2 $ thì thể tích khối tứ diện $ABCD$ đạt giá trị lớn nhất.

Câu 3. Lạm phát là sự tăng mức giá chung một cách liên tục của hàng hoá và dịch vụ theo thời gian, tức là sự mất giá trị của một loại tiền tệ nào đó. Chẳng hạn, nếu lạm phát là $5% $ một năm thì sức mua của 1 triệu đồng sau một năm chỉ còn là 950 nghìn đồng (vì đã giảm mất $5% $ của 1 triệu đồng, tức là 50000 đồng). Nói chung, nếu tỉ lệ lạm phát trung bình là $r% $ một năm thì tổng số tiền $P$ ban đầu, sau $n$ năm số tiền đó chỉ còn giá trị là: $A = P{left( {1 – frac{r}{{100}}} right)^n}$

a) Nếu tỉ lệ lạm phát là $7% $ một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại 86490000 đồng.

B) Nếu tỉ lệ lạm phát là 7% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại 96490000 đồng.

c) Nếu sức mua của 100 triệu đồng sau ba năm chỉ còn lại 80 triệu đồng thì tỉ lệ lạm phát trung bình của ba năm đó là $9,17% $ (làm tròn kết quả đến hàng phần trăm)?

d) Nếu tỉ lệ lạm phát trung bình là $6% $ một năm thì sau 15 năm sức mua của số tiền ban đầu chỉ còn lại một nửa

Câu 4.Cho hàm số $y = si{n^2}x$. Các mệnh đề sau đúng hay sai?

a) $2y’ + y” = sqrt 2 cosleft( {2x – frac{pi }{4}} right)$.

b) $2y + y’ cdot tanx = 0$.

c) $4y – y” = 2$.

d) $4y’ + y”’ = 0$.

Phần 3. Câu trả lời ngắn.
Thí sinh trả lờ đáp án từ câu 1 đến câu 6.

Câu 1.Khi tung một đồng xu không cân đối thì người ta thấy rằng xác suất để đồng xu xuất hiện mặt sấp bằng $frac{2}{3}$. Tung đồng xu này ba lần liên tiếp. Tính xác suất để xuất hiện 2 lần mặt sấp, 1 lần mặt ngửa;

Câu 2.Một lớp học có 40 học sinh trong đó có 25 học sinh thích môn Toán, 20 học sinh thích môn Ngữ văn và 12 học sinh thích cả hai môn Ngữ văn và Toán. Tính xác suất để chọn được một học sinh thích môn Ngữ văn mà không thích môn Toán.

Câu 3.Cho hình lăng trụ đứng $ABC cdot A’B’C’$ có đáy là tam giác vuông cân tại $B,AC = 2a$ và $A’B = 3a$. Tính góc phẳng nhị diện $left[ {B’,AC,B} right]$ ?

Câu 4. Cho khối lăng trụ đứng $ABC cdot A’B’C’$ có đáy là tam giác vuông cân tại $A,BC = 2a$ và $A’C = asqrt 7 $. Tính thể tích khối lăng trụ đã cho.

Câu 5.Một quần thể của loài ong mật lớn lên tại một nhà nuôi ong bắt đầu với 50 con ong, tại thời điểm $t$ số lượng ong của quần thể này được mô hình hóa bởi công thức: $Pleft( t right) = frac{{7520}}{{1 + 1503{e^{ – 0,5932t}}}}$. trong đó tlà thời gian được tính bằng tuần. Hỏi sau bao lâu thì quần thể ong có tốc độ phát triển nhanh nhất.

Câu 6. Một chất điểm chuyển động theo phương trình $S = – {t^3} + 3{t^2} – 2$, trong đó $t$ tính bằng giây và $S$ tính theo mét. Vận tốc lớn nhất của chuyển động chất điểm đó là bao nhiêu?

ĐÁP ÁN VÀ LỜI GIẢI THAM KHẢO

Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án đúng nhất.

1B	2D	3C	4D	5C	6B
7C	8A	9A	10C	11B	12C

Câu 1.Trong các khẳng định sau khẳng định nào sai?

A. ${2^{30}} < {3^{20}}$.

B. $0,{99^pi } > 0,{99^e}$.

C. $lo{g_{{a^2} + 2}}left( {{a^2} + 1} right) geqslant 0$.

D. ${4^{ – sqrt 3 }} < {4^{ – sqrt 2 }}$.

Lời giải

Ta có: $pi > e$ và $0,999 < 1$ nên $0,{99^pi } < 0,{99^e}$, do đó đáp án $B$ sai.

Câu 2.Đồ thị (hình bên) là đồ thị của hàm số nào ?

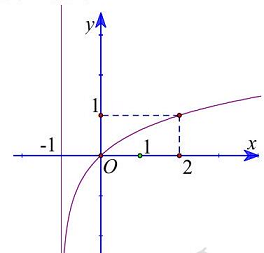
A. $y = {log_2}x + 1$.

B. $y = {log_2}left( {x + 1} right)$.

C. $y = {log_3}x$.

D. $y = {log_3}left( {x + 1} right)$.

Lời giải

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số nhận đường thẳng $x = – 1$ làm tiệm cận đứng nên loại đáp án $A$ và $C$.

Lại có $Aleft( {2;1} right)$ thuộc đồ thị hàm số nên loại phương án $B$.

Câu 3. Tập nghiệm của bất phương trình $lo{g_{frac{1}{2}}}left( {{x^2} – x + 7} right) > 0$ là

A. $left( { – infty ;2} right) cup left( {3; + infty } right)$.

B. $left( { – infty ;2} right)$.

C. $left( {2;3} right)$.

D. $left( {3; + infty } right)$.

Lời giải

$lo{g_{frac{1}{2}}}left( {{x^2} – x + 7} right) > 0 Leftrightarrow left{ {begin{array}{*{20}{l}}
{{x^2} – 5x + 7 > 0} \
{{x^2} – 5x + 7 < 1}
end{array} Leftrightarrow left{ {begin{array}{*{20}{l}}
{{{left( {x – frac{5}{2}} right)}^2} + frac{3}{4} > 0,forall x in mathbb{R}} \
{{x^2} – 5x + 6 < 0}
end{array} Rightarrow x in left( {2;3} right)} right.} right.$.

Câu 4. Cho hình lập phương $ABCD cdot A’B’C’D’$. Góc giữa hai đường thẳng $A’C’$ và $BD$ bằng.

A. ${60^ circ }$.

B. ${30^ circ }$.

C. ${45^ circ }$.

D. ${90^ circ }$.

Lời giải

Ta có: $left( {widehat {A’C’;BD}} right) = left( {widehat {AC;BD}} right) = {90^ circ }$

Câu 5. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a,SA bot left( {ABCD} right)$ và $SA = asqrt 3 $ Gọi $alpha $ là góc tạo bởi giữa đường thẳng $SB$ và mặt phẳng $left( {SAC} right)$, khi đó $alpha $ thỏa mãn hệ thức nào sau đây:

A. $cosalpha = frac{{sqrt 2 }}{8}$.

B. $sinalpha = frac{{sqrt 2 }}{8}$.

C. $sinalpha = frac{{sqrt 2 }}{4}$.

D. $cosalpha = frac{{sqrt 2 }}{4}$.

Lời giải

Gọi $O$ là tâm của đáy $ABCD$.

Ta có $BO bot AC$ và $BO bot SA$ nên $SO$ là hình chiếu của $SB$ trên $left( {SAC} right)$.

Suy ra $alpha = widehat {BSO}$.

Lai có $BO = frac{{asqrt 2 }}{2},SB = sqrt {S{A^2} + A{B^2}} = 2a$. Suy ra $sinalpha = frac{{BO}}{{SB}} = frac{{sqrt 2 }}{4}$.

Câu 6.Cho hình lập phương $ABCD cdot A’B’C’D’$. Khẳng định nào sau đây sai?

A. $mpleft( {AA’C’C} right) bot mpleft( {ABCD} right)$.

B. $mpleft( {ABB’A’} right) bot mpleft( {BDD’B’} right)$.

C. $mpleft( {ABB’A’} right) bot mpleft( {A’B’C’D’} right)$.

D. $mpleft( {ACC’A’} right) bot mpleft( {BB’D’D} right)$.

Chọn B

Lời giải

$left{ {begin{array}{*{20}{l}}
{mpleft( {ABB’A’} right) cap mpleft( {BDD’B’} right) = BB’} \
{AB bot BB’} \
{DB bot BB’}
end{array}} right.$

$ Rightarrow left( {mpleft( {ABB’A’} right),mpleft( {BDD’B’} right)} right) = widehat {left( {AB,DB} right)} = {45^0}$.

Câu 7. Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc nhau và $OA = OB = OC = 3a$. Tính khoảng cách giữa hai đường thẳng $AC$ và $OB$.

A. $frac{{3a}}{2}$.

B. $frac{{asqrt 2 }}{2}$.

C. $frac{{3asqrt 2 }}{2}$.

D. $frac{{3a}}{4}$.

Lời giải

Gọi $M$ là trung điểm của $AC Rightarrow AC bot OM Rightarrow OM$ là đường vuông góc chung của $AC$ và $OB,AC = 3asqrt 2 Rightarrow OM = frac{{3asqrt 2 }}{2}$.

Câu 8.Cho hình chóp $S.ABC$ có $SA$ vuông góc mặt đáy, tam giác $ABC$ vuông tại $A,SA = 2;cm$, $AB = 4;cm,AC = 3;cm$. Tính thể tích khối chóp $S.ABC$.

A. $frac{{12}}{3};c{m^3}$.

B. $frac{{24}}{5};c{m^3}$.

C. $frac{{24}}{3};c{m^3}$.

D. $24;c{m^3}$.

Lời giải

${V_{S.ABC}} = frac{1}{3} cdot SA cdot {S_{vartriangle ABC}} = frac{1}{3} cdot 2 cdot frac{1}{2} cdot 4 cdot 3 = 4left( {;c{m^3}} right).$

Câu 9.Nhi và Nhung thường xuyên đến cùng một quán cà phê cùng khung giờ, tuy nhiên hai bạn không đi cùng nhau. Nhi thường đến vào 2 ngày bất kỳ trong tuần, Nhung thì thường đến 3 ngày bất kỳ. Tính xác suất hai bạn gặp được nhau.

A. $P = frac{6}{{49}}$.

B. $P = frac{8}{{49}}$.

C. $P = frac{{15}}{{49}}$.

D. $P = frac{{20}}{{49}}$.

Lời giải

Xác suất Nhi đến quán cà phê là $frac{2}{7}$.

Xác suất Nhung đến quán cà phê là $frac{3}{7}$.

Xác suất để hai bạn gặp nhau là $frac{2}{7} cdot frac{3}{7} = frac{6}{{49}}$.

Chọn A.

Câu 10.Tung một đồng xu 3 lần. Xác suất đồng xu xuất hiện 2 lần mặt ngửa và một lần mặt sấp là:

A. $frac{1}{4}$.

B. $frac{2}{3}$.

C. $frac{3}{8}$.

D. $frac{1}{2}$.

Lời giải

Các trường hợp có thể xảy ra là: $SSS,SSN,SNS,SNN,NSS,NSN,NNS,NNN$.

Xác suất đồng xu xuất hiện 2 lần mặt ngửa và một lần mặt sấp là $frac{3}{8}$.

Chọn C.

Câu 11. Tìm đạo hàm của hàm số $y = x{e^x}$

A. $1 + {e^x}$.

B. $left( {1 + x} right){e^x}$.

C. $left( {1 – x} right){e^x}$.

D. ${e^x}$.

Lời giải

Ta có ${left( {x{e^x}} right)’} = {(x)’} cdot {e^x} + x cdot {left( {{e^x}} right)’} = {e^x} + x cdot {e^x} = left( {1 + x} right){e^x}$.

Câu 12. Cho hàm số $y = – 2{x^3} + 6{x^2} – 5$ có đồ thị $left( C right)$. Phương trình tiếp tuyến của $left( C right)$ tại điểm $M$ thuộc $left( C right)$ và có hoành độ bằng 3 là

A. $y = 18x – 49$.

B. $y = – 18x – 49$.

C. $y = – 18x + 49$.

D. $y = 18x + 49$.

Lời giải

$y’ = f’left( x right) = – 6{x^2} + 12x$, giả sử điểm $Mleft( {{x_0};{y_0}} right)$ thì ${x_0} = 3 Rightarrow {y_0} = – 5,f’left( 3 right) = – 18$

Vậy phương trình tiếp tuyến $y = f’left( {{x_0}} right)left( {x – {x_0}} right) + {y_0} = – 18left( {x – 3} right) – 5 = – 18x + 49$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1.Một hộp chứa 15 viên bi xanh và 20 viên bi đỏ, có cùng kích thước và khối lượng. Lần lượt lấy ngẫu nhiên ra 2 viên bi, mỗi lần một viên. Gọi $A$ là biến cố “Lấy được viên bi màu xanh ở lần thứ nhất” và $B$ là biến cố “Lấy được viên bi màu xanh ở lần thứ hai”. Khi đó:

a) Hai biến cố $A$ và $B$ không độc lập

b) $Pleft( {AB} right) = frac{3}{{17}}$

c) $Pleft( {Aoverline B } right) = frac{{60}}{{119}}$

d) Xác suất để hai viên bi lấy ra khác màu là: $frac{{30}}{{119}}$

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Sai

a) Hai biến cố $A$ và $B$ không độc lập vì việc lần đầu lấy được bi xanh hay không sẽ ảnh hưởng đến việc lần sau lấy bi.

b) Ta có $Pleft( {AB} right) = frac{{15}}{{35}} cdot frac{{14}}{{34}} = frac{3}{{17}}$.

d) Xác suất để hai viên bi lấy ra khác màu là:

$Pleft( {Aoverline B } right) + Pleft( {overline A B} right) = frac{{15}}{{35}} cdot frac{{20}}{{34}} + frac{{20}}{{35}} cdot frac{{15}}{{34}} = frac{{60}}{{119}}.$

Câu 2. Xét khối tứ diện $ABCD$ có cạnh $AB = x$, các cạnh còn lại đều bằng $2sqrt 3 $. Các mệnh đề sau đúng hay sai?

a) Diện tích tam giác $BCD$ bằng ${S_{BCD}} = 3sqrt 3 $

b) ${V_{ABCD}} = frac{{sqrt 3 }}{3}xsqrt {36 – {x^2}} $

c) Khi $x = 3$ thì $V = frac{9}{4}$

d) Khi $x = 3sqrt 2 $ thì thể tích khối tứ diện $ABCD$ đạt giá trị lớn nhất.

Lời giải

a) Đúng

b) Sai

c) Sai

d) Đúng

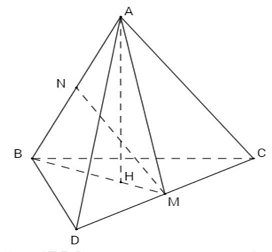
Gọi $M,N$ lần lượt là trung điểm $CD$ và $AB;H$ là hình chiếu vuông góc của $A$ lên $BM$.

Ta có: $left. {begin{array}{*{20}{l}}
{CD bot BM} \
{CD bot AM}
end{array}} right} Rightarrow CD bot left( {ABM} right) Rightarrow left( {ABM} right) bot left( {ABC} right)$.

Mà $AH bot BM;BM = left( {ABM} right) cap left( {ABC} right) Rightarrow AH bot left( {ABC} right)$.

Do $ACD$ và $BCD$ là hai tam giác đều cạnh $2sqrt 3 Rightarrow AM = BM = frac{{sqrt 3 }}{2} cdot 2sqrt 3 = 3$.

Tam giác $AMN$ vuông tại $N$, có: $MN = sqrt {A{M^2} – A{N^2}} = sqrt {9 – frac{{{x^2}}}{4}} $.

Lại có: ${S_{BCD}} = frac{{sqrt 3 }}{4}{(2sqrt 3 )^2} = 3sqrt 3 $.

${V_{ABCD}} = frac{1}{3}AH cdot {S_{BCD}} = frac{1}{3} cdot frac{{xsqrt {36 – {x^2}} }}{6} cdot 3sqrt 3 = frac{{sqrt 3 }}{6}xsqrt {36 – {x^2}} $.

Ta có: ${V_{ABCD}} = frac{{sqrt 3 }}{6}xsqrt {36 – {x^2}} leqslant frac{{sqrt 3 }}{6} cdot frac{{{x^2} + 36 – {x^2}}}{2} = 3sqrt 3 $.

Suy ra ${V_{ABCD}}$ lớn nhất bằng $3sqrt 3 $ khi ${x^2} = 36 – {x^2} Rightarrow x = 3sqrt 2 $.

Câu 3. Lạm phát là sự tăng mức giá chung một cách liên tục của hàng hoá và dịch vụ theo thời gian, tức là sự mất giá trị của một loại tiền tệ nào đó. Chẳng hạn, nếu lạm phát là $5% $ một năm thì sức mua của 1 triệu đồng sau một năm chỉ còn là 950 nghìn đồng (vì đã giảm mất $5% $ của 1 triệu đồng, tức là 50000

đồng). Nói chung, nếu tỉ lệ lạm phát trung bình là $r% $ một năm thì tổng số tiền $P$ ban đầu, sau $n$ năm số

tiền đó chỉ còn giá trị là: $A = P{left( {1 – frac{r}{{100}}} right)^n}$

a) Nếu tỉ lệ lạm phát là 7% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại 86490000 đồng.

B) Nếu tỉ lệ lạm phát là 7% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại 96490000 đồng.

c) Nếu sức mua của 100 triệu đồng sau ba năm chỉ còn lại 80 triệu đồng thì tỉ lệ lạm phát trung bình của ba năm đó là $9,17% $ (làm tròn kết quả đến hàng phần trăm)?

d) Nếu tỉ lệ lạm phát trung bình là $6% $ một năm thì sau 15 năm sức mua của số tiền ban đầu chỉ còn lại một nửa

Hướng dẫn giải

Lời giải

a) Đúng

b) Sai

c) Sai

d) Sai

a) b) Giả thiết cho $P = 100$ triệu đồng, $r% = 7% ,n = 2$ năm.

Ta có: $A = {100.10^6}{left( {1 – frac{7}{{100}}} right)^2} = 86490000$ đồng.

Vậy sau hai năm sức mua còn lại của 100000000 là 86490000 dồng.

c) Giả thiết cho $P = 100$ triệu đồng, $A = 80$ triệu đồng, $n = 3$ năm.

Ta có: $80 = 100{left( {1 – frac{r}{{100}}} right)^3} Leftrightarrow 1 – frac{r}{{100}} = sqrt[3]{{frac{4}{5}}} Leftrightarrow r approx 7,17$.

Vậy tỉ lệ lạm phát trung bình của ba năm là $r% approx 7,17% $.

d) Giả thiết cho $P = X$ triệu đồng, $A = frac{X}{2}$ triệu đồng, $r% = 6% $.

Ta có: $frac{X}{2} = X{left( {1 – frac{6}{{100}}} right)^n} Leftrightarrow {(0,94)^n} = frac{1}{2} Leftrightarrow n approx 11,2$ (năm).

Vậy sau khoảng 12 năm sức mua của số tiền còn lại là một nửa.

Câu 4.Cho hàm số $y = si{n^2}x$. Các mệnh đề sau đúng hay sai?

a) $2y’ + y” = sqrt 2 cosleft( {2x – frac{pi }{4}} right)$.

b) $2y + y’ cdot tanx = 0$.

c) $4y – y” = 2$.

d) $4y’ + y”’ = 0$.

Lời giải

a) Sai

b) Sai

c) Sai

d) Đúng

Ta có $y’ = sin2x,y” = 2cos2x,y”’ = – 4sin2x$

$2y’ + y” = 2left( {sin2x + cos2x} right) = 2sqrt 2 cosleft( {2x – frac{pi }{4}} right)$

$2y + y’ cdot tanx = 2si{n^2}x + 2sinx cdot cosx cdot tanx = 4si{n^2}x,$

$4y – y” = 4si{n^2}x – 2cos2x = 2 – 4cos2x$

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1.Khi tung một đồng xu không cân đối thì người ta thấy rằng xác suất để đồng xu xuất hiện mặt sấp bằng $frac{2}{3}$. Tung đồng xu này ba lần liên tiếp. Tính xác suất để xuất hiện 2 lần mặt sấp, 1 lần mặt ngửa;

Trả lời: $frac{4}{9}$

Lời giải

Xác suất chỉ xuất hiện 2 lần mặt sấp, 1 lần mặt ngửa là: $C_3^2{left( {frac{2}{3}} right)^2} cdot frac{1}{3} = frac{4}{9}$.

Câu 2. Một lớp học có 40 học sinh trong đó có 25 học sinh thích môn Toán, 20 học sinh thích môn Ngữ văn và 12 học sinh thích cả hai môn Ngữ văn và Toán. Tính xác suất để chọn được một học sinh thích môn Ngữ văn mà không thích môn Toán.

Trả lời: $frac{8}{{40}}$

Lời giải

Xác suất để chọn được một học sinh thích môn Ngữ văn mà không thích môn Toán: $frac{8}{{40}}$.

Câu 3.Cho hình lăng trụ đứng $ABC cdot A’B’C’$ có đáy là tam giác vuông cân tại $B,AC = 2a$ và $A’B = 3a$. Tính góc phẳng nhị diện $left[ {B’,AC,B} right]$ ?

Trả lời: $69,{3^ circ }$

Lời giải

Ta có: $left{ {begin{array}{*{20}{l}}
{left( {B’AC} right) cap left( {ABC} right) = AC} \
{Trongleft( {ABC} right),BI bot AC} \
{Trongleft( {B’AC} right),B’I bot AC}
end{array}} right.$$ Rightarrow left[ {A,SC,B} right] = widehat {B’IB}$

Ta có: $BI = frac{{AC}}{2} = a$

$B’B = sqrt {{{(3a)}^2} – {{(asqrt 2 )}^2}} = sqrt 7 a$

Xét $vartriangle BB’I$ vuông tại $B:tanwidehat {B’IB} = frac{{B’B}}{{BI}} = frac{{sqrt 7 a}}{a} = sqrt 7 Rightarrow widehat {B’IB} approx 69,{3^ circ }$

Câu 4.Cho khối lăng trụ đứng $ABC cdot A’B’C’$ có đáy là tam giác vuông cân tại $A,BC = 2a$ và $A’C = asqrt 7 $. Tính thể tích khối lăng trụ đã cho.

Trả lời: $sqrt 5 {a^3}$

Lời giải

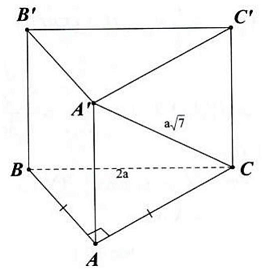
$V = {S_{ABC}} cdot A’A$

$AB = AC = frac{{2a}}{{sqrt 2 }} = sqrt 2 a$

${S_{ABC}} = frac{{{{(sqrt 2 a)}^2}}}{2} = {a^2}$

$A’A = sqrt {A'{C^2} – A{C^2}} = sqrt {{{(asqrt 7 )}^2} – {{(sqrt 2 a)}^2}} = sqrt 5 a$

$ Rightarrow {V_{S.ABC}} = {a^2} cdot sqrt 5 a = sqrt 5 {a^3}$

Câu 5.Một quần thể của loài ong mật lớn lên tại một nhà nuôi ong bắt đầu với 50 con ong, tại thời điểm $t$ số lượng ong của quần thể này được mô hình hóa bởi công thức: $Pleft( t right) = frac{{7520}}{{1 + 1503{e^{ – 0,5932t}}}}$. trong đó tlà thời gian được tính bằng tuần. Hỏi sau bao lâu thì quần thể ong có tốc độ phát triển nhanh nhất.

Trả lời: 12,332 tuần

Lời giải

Ta có: $P’left( t right) = frac{{7520.1503 cdot 0,5932 cdot {e^{ – 0,5932t}}}}{{1 + 1503{e^{ – 0,5932t}}}}$.

$P”left( t right) = frac{{7520 cdot 1503 cdot {{(0,5932)}^2} cdot {e^{ – 0,5932t}}left( { – 1 + 1503{e^{ – 0,5932t}}} right)}}{{{{left( {1 + 1503{e^{ – 0,5932t}}} right)}^3}}}$

$ Rightarrow P”left( t right) = 0 Leftrightarrow 1503{e^{ – 0,5932t}} = 1$$ Leftrightarrow {e^{ – 0,5932t}} = frac{1}{{1503}} Leftrightarrow t = frac{{ln1503}}{{0,5932}} approx 12,332$

Câu 6.Một chất điểm chuyển động theo phương trình $S = – {t^3} + 3{t^2} – 2$, trong đó $t$ tính bằng giây và $S$ tính theo mét. Vận tốc lớn nhất của chuyển động chất điểm đó là bao nhiêu?

Trả lời: $3;m/s$

Ta có: $v = S’ = – 3{t^2} + 6t$.

Lời giải

${v_{max}} Leftrightarrow t = frac{{ – b}}{{2a}} = 1left( s right)$

$ Rightarrow {v_{max}} = vleft( 1 right) = 3m/s$.