Cách Tìm Tiệm Cận Đứng Ngang Dựa Vào Bảng Biến Thiên

Cách tìm tiệm cận đứng ngang dựa vào bảng biến thiên được soạn dưới dạng file word và PDF gồm 3 trang. Các bạn xem và tải về ở dưới.

I. Tìm tiệm cận đứng của đồ thị hàm số dựa vào bảng biến thiên

1. Phương pháp

Bước 1: Tìm các giá trị ${x_0}$ mà hàm số không xác định (Dấu hai gạch dọc).

Bước 2: Sử dụng định nghĩa đường tiệm cận đứng.

Đường thẳng $x = {x_0}$ được gọi là đường tiệm cận đứng của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong các điều kiện sau đây thỏa mãn:

$mathop {lim }limits_{x to {x_0}^ + } f(x) =  + infty $; $mathop {lim }limits_{x to {x_0}^ + } f(x) =  – infty $; $mathop {lim }limits_{x to {x_0}^ – } f(x) =  + infty $; $mathop {lim }limits_{x to {x_0}^ – } f(x) =  – infty $.

2. Các ví dụ

Ví dụ 1.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận đứng của đồ thị hàm số $y = f(x)$.

Lời giải

Hàm số không xác định tại ${x_0} = 6$.

Ta có:

$mathop {lim }limits_{x to {6^ + }} y = – infty $; $mathop {lim }limits_{x to {6^ + }} y = + infty $

$ Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 6$

Ví dụ 2.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận đứng của đồ thị hàm số $y = f(x)$.

Lời giải

Hàm số không xác định tại ${x_0} = – 7$ và ${x_0} = 4$.

* Ta có:

$mathop {lim }limits_{x to – {7^ + }} y = + infty $; $mathop {lim }limits_{x to – {7^ – }} y = 9$

$ Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = – 7$.

* Ta có:

$mathop {lim }limits_{x to {4^ + }} y = 2$; $mathop {lim }limits_{x to {4^ – }} y = 1$

$ Rightarrow $ Đường thẳng $x = 4$ không phải là tiệm cận đứng của đồ thị hàm số.

Vậy, hàm số có tiệm đứng là $x = – 7$.

Ví dụ 3.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận đứng của đồ thị hàm số $y = f(x)$.

Lời giải

Hàm số không xác định tại ${x_0} = 1$ và ${x_0} = 5$.

* Ta có:

$mathop {lim }limits_{x to {1^ + }} y = 3$; $mathop {lim }limits_{x to {1^ – }} y = + infty $

$ Rightarrow $ Đường thẳng $x = 1$ là tiệm cận đứng của đồ thị hàm số.

* Ta có:

$mathop {lim }limits_{x to {5^ + }} y = 0$; $mathop {lim }limits_{x to {5^ + }} y = – infty $

$ Rightarrow $ Đường thẳng $x = 5$ là tiệm cận đứng của đồ thị hàm số.

Vậy, hàm số có hai tiệm đứng là $x = 1$; $x = 5$.

II. Tìm tiệm cận ngang của đồ thị hàm số

1. Phương pháp:

Sử dụng định nghĩa: Đường thẳng $y = {y_0}$ được gọi là đường tiệm cận ngang của đồ thị hàm số $y = f(x)$ nếu $mathop {lim }limits_{x to  + infty } f(x) = {y_0}$ hoặc $mathop {lim }limits_{x to  – infty } f(x) = {y_0}$.

2. Các ví dụ

Ví dụ 4.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.

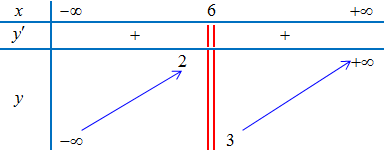
Lời giải

Ta có:

$mathop {lim }limits_{x to + infty } y = + infty $; $mathop {lim }limits_{x to – infty } y = – infty $

$ Rightarrow $ Đồ thị hàm số không có tiệm cận ngang.

Ví dụ 5.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.

Lời giải

Ta có:

$mathop {lim }limits_{x to + infty } y = 10$; $mathop {lim }limits_{x to – infty } y = – infty $

$ Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = 10$.

Ví dụ 6.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.

Lời giải

Ta có:

$mathop {lim }limits_{x to + infty } y = – 5$; $mathop {lim }limits_{x to – infty } y = – 5$

$ Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = – 5$.

Ví dụ 7.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.

Lời giải

Ta có:

$mathop {lim }limits_{x to + infty } y = 9$; $mathop {lim }limits_{x to – infty } y = – 2$

$ Rightarrow $ Đồ thị hàm số có hai tiệm cận ngang là đường thẳng $y = 9$ và $y = – 2$.

Chú ý: Đồ thị hàm số $y = f(x)$ có tối đa hai tiệm cận ngang.

Ví dụ 8.Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.

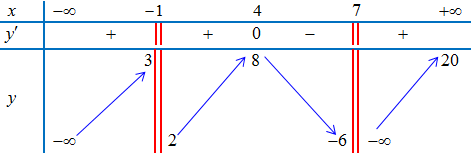
Lời giải

* Tìm tiệm cận đứng

Hàm số không xác định tại ${x_0} = – 1$và ${x_0} = 7$.

Ta có:

$mathop {lim }limits_{x to – {1^ + }} y = 2$; $mathop {lim }limits_{x to – {1^ – }} y = 3$

$ Rightarrow $ Đường thẳng $x = – 1$ không phải là tiệm cận đứng của đồ thị hàm số.

$mathop {lim }limits_{x to {7^ + }} y = – infty $; $mathop {lim }limits_{x to {7^ + }} y = – 6$

$ Rightarrow $ Đường thẳng $x = 7$ là tiệm cận đứng của đồ thị hàm số.

* Tìm tiệm cận ngang

Ta có:

$mathop {lim }limits_{x to + infty } y = 20$; $mathop {lim }limits_{x to – infty } y = – infty $

$ Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = 20$.

Vậy, đồ thị hàm số có tiệm cận đứng là đường thẳng $x = 7$ và tiệm cận ngang là đường thẳng $y = 20$.